Средняя линия трапеции равна 12 см. Найдите большее основание трапеции, если основания относятся как 1:5

Решение:
Пусть меньше основание трапеции будет х см, тогда и соотношения оснований второе - больше основание будет 5х см. так как средняя линия трапеции равна полусумме оснований, то составим равенство: (х+5х):2=12 6х:2=12 6х=24 х=4 см - меньше основание 4*5=20 см - больше основание

Средняя линяя трапеции равна 18, а одно из её оснований больше другого на 16. Найдите меньшее основание трапеции.

Пусть меньшее основание х, тогда большее равно х+16. По свойству средней линии трапеции: 2·18 = х + (х+16), отсюда х = 10. Ответ: 10.

Длины оснований трапеции относятся как 7:3, и их разность равна 3,2 м. Найдите длину средней линии этой трапеции.

Пусть а и в - основания трапеции. Можно записать уравнения: а/в=7/3 и а-в=3,2, выразим а из первого и подставим во второе: а=7в/3; 7в/3-в=3,2; в=2,4; а=7в/3=7*2,4/3=5,6.
Теперь средняя линия: с=(а+в)/2=(5,6+2,4)/2=4.

Ответ: 4.

Диагональ равнобокой трапеции перпендикулярна боковой стороне и относится к ней как 4:3. Большее основание трапеции равно 50см. Найдите среднюю линию трапеции.

Пусть ABCD- трапеция
Треугольник ABD- прямоугольный
AB=3x, BD=4x, где х- коэффициент пропорциональности
тогда по теореме Пифагора
    (3x)^2+(4x)^2=(50)^2
     9x^2+16x^2=2500
     25x^2=2500
     x^2=100
     x=10
то есть AB=3*x=30
            BD=4*x=40
Из вершины B опустим перпендикуляр BK на AD
Если высота проведена из прямого угла, то она равна произведению катетов, деленное на гипотенузу
то есть
   BK=AB*BD/AD=30*40/50= 24
тогда из треугольника ABK
    (AK)^2=(AB)^2-(BK)^2=900-576=324 => AK=18
BC=AD-2*AK=50-36=14
Пусть k- средняя линия трапеции, тогда k=(BC+AD)/2=(14+50)/2=64/2=32

В равнобедренной трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если её периметр равен 48, а большее основание 18

Трапеция АВСД, АВ=СД, АД=18, АС - диагональ = биссектриса угла А,
угол САД=углу АСВ как внутренние разносторонние = углу САВ, треугольник АВС - равнобедренный, АВ = ВС = СД
периметр=АВ+ВС+СД+АД
48 = 3АВ + 18
3АВ = 30, АВ = ВС = СД = 30/3 = 10
Средняя линия =(АД+ВС)/2=(18+10)/2=14

Диагональ равнобокой трапеции перпендикулярна боковой стороне и относится к ней как 4:3. Большее основание трапеции равно 50 см. Найдите среднюю линию трапеции.

Пусть АВСD трапеция и AD  большее основание, тогда ВС меньшее, так как у нас угол прямой,  то  треугольник   ACD  прямоугольный пусть диагональ равна 4х, то боковая  сторона равна 3х
по теореме Пифагора получаем
 (3x)^2+(4x)^2=50^2
 25x^2=2500
 x=10
 то есть сторона равна 30, а диагональ равна 40.  Можно провести высоту,  а высота в прямоугольном треугольнике равна произведению катетов на гипотенузу H=ab/c  = 40*30/50 = 24,  у нас трапеция равнобедренная, боковые стороны равны  30.
Высота наша CH, то AH=√40^2-24^2 = 32. Соответственно  HD=50-32 =18.
BC=AH-HD=32-18 =  14
средняя линия трапеций равна полусумме оснований то есть  m=(14+50)/2 =32
 Ответ 32 см 

Меньшее основание трапеции относится к средней линии как 1:3, а большее основание равно 30 см. Найдите среднюю линию трапеции

Пусть меньшее основание х
ср линия тогда, следуя из условия, 3х
большее основание 30
пропорция  3х=х+30\2                6х=х+30          5х=30       х=6          ср линия =6*3=18           Ответ 18

или так:

Средняя линия = полусумма оснований, пусть MN-средняя линия, AB и CD-большее и меньшее основания соответственно
MN=(AB+CD)/2
MN=(1/3MN+CD)/2
MN=1/6MN+15
5/6MN=15
MN=18

Основание трапеции относятся как 2:3. Её средняя линия равна 24дм. Найдите основания трапеции.

Средняя линия трапеции равна полусумме её оснований. 24*2 =(2х+3х)
48=5х
х=9,6 дм. Ответ:9,6 дм.

1) Основание трапеции относится как 1:11, а средняя линия рана 48. Найти большее основание трапеции.
2) Средняя линия трапеции равна 11, одно из ее оснований больше другого на 12. Найдите меньшее основание.

1) Возьмем 1 часть за х
Исходя из формулы средней линии составим уравнение:
(х + 11х) /2 = 48. Чтобы избавиться от знаменателя 2, домножим обе части уравнения на 2.
х + 11х = 96
12х = 96
х = 8.
Малое основание = 8, большее = 11*-8=88.
2) Тоже самое, но здесь будет другое уравнение:
(х + 12 + х) / 2 = 11. Так же домножим на 2.
х + 12 + х =22
2х= 10
х= 5
Малое основание = 5, большее= 12 + 5 = 17.

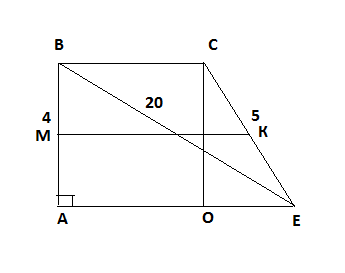
Боковые стороны прямоугольной трапеции относятся как 4:5, а одно из оснований на 9 см больше другого. Большая диагональ трапеции равна 20 см. Найдите среднюю линию трапеции.

Зная разницу большего и меньшего оснований, запишем, что ОЕ=9 см
АВ/СЕ = 4/5, отсюда СЕ = АВ*5/4
Рассмотрим прямоугольный треуг-ик СОЕ. Здесь СО = АВ. Пользуясь теоремой Пифагора, запишем:
СО²=СЕ²-ОЕ², или с учетом того, что СО=АВ запишем:
АВ²=СЕ²-ОЕ²=(АВ*5/4)²-81=25АВ²/16-81
16АВ²=25АВ²-1296
25АВ²-16АВ²=1296
9АВ²=1296
АВ²=144
АВ=12 см
В прямоугольном треуг-ке ВАЕ по теореме Пифагора находим катет АЕ:
AE=√BE²-AB²=√400-144=√256=16 см
ВС=АЕ-9=16-9=7 см
МК=(ВС+АЕ):2=(7+16):2=11.5 см