Найдите длину хорды, что проведена в кругу радиусом 15 см на расстояние 12 см от центра круга

Решение:
Отметим центр круга как O. Проведем два произвольных радиуса OA и OB, отрезок AB - хорда, центр хорды - H
Решение: Расстояние от хорды до центра окружности проходит под прямым углом по центру отрезка AB (AH перпендикулярно AB и AH=BH). OBH = OAH. По теореме Пифагора находим AH и BH: AH=sqr(15^2-12^2)=9 см Ответ: AH=B=9 см.
(Для плохо знающих ИКТ на будущее SQR - квадратный корень, ^ - степень)
 

В окружности радиуса 5 см на расстоянии 3 см от центра проведена хорда. Найдите длину хорды.

Т.к. от центра окружности до хорды расстояние, то это перпендикуляр. Проведем 2 радиуса к точка пересечения хорды с окружностью. Получим равнобедренный треугольник с боковой стороной 5 и высотой 3 и основанием которая является хордой. По т. Пифагора найдем половину основания треугольника = 4, а следовательно основание треугольника 8

К окружности проведены касательные МА и МВ (А и В – точки касания). Найдите длину хорды АВ, если радиус окружности равен 20 см, а расстояние от точки М до хорды АВ равно 9 см.

Точка С - средина хорды АВ.
 МС = 9 МС пересекает окружность в точке Н
Продолжение МС проходит через центр окружности затем пересекает окружность в точке К
НК = диаметр = 2 · 20 = 40 СА = СВ СА^2 = CB^2 = CH · CК МА^2 = МН · МК
МА^2 - CA^2 = МС^2 МН · МК - CH · CК = 9^2 ( уравнение 1 ) МН = МС - СН = 9 - СН МК = МС + НК - СН = 9 + 40 - СН = 49 - СН СК = НК - СН = 40 - СН СН заменим на Х и подставим всё в уравнение 1 ( 9 - Х ) * ( 49 - Х ) - Х * ( 40 - Х ) = 81 441 - 58Х + Х^2 - 40X + X^2 = 81 2X^2 - 98X + 360 = 0 a = 2, b = -98, c = 360 D = b^2 - 4 * a * c = ( -98 )^2 - 4 * 2 * 360 = 9604 - 2880 = 6724 корень квадратный D = 82 X1 = ( -b + к. К. D ) / (2*a) = ( 98 + 82 ) / (2*2) = 45 ( не подходит так как СН меньше МС значит СН меньше 9 ) Х2 = ( -b - к. К. D ) / (2*a) = ( 98 - 82 ) / (2*2) = 4 CH = X = 4 CК = НК - СН = 40 - 4 = 36 СА = кор. Кв. ( СН * СК ) = кор. Кв ( 4 * 36 ) = кор. Кв 144 = 12 Хорда АВ = СА * 2 = 12 * 2 = 24

---

Отрезки касательных к окружности проведенные из одной точки равны и составляют равные углы с прямой проходящей через эту точку и центр окружности, значит МА=МВ.   расстояние от точки M до хорды AB равное 9 есть перпендикуляр МН к хорде АВ, угол АМН=ВМН. НА=НВ=0,5АВ. Пусть АН=НВ=х. По теореме Пифагора МА=√x^2+81, MO=9+√400-x^2. Площадь треугольника МАО равна половине произведения его катетов МА и МО а также поделив пополам произведение гипотенузы на высоту к гипотенузе MO * AН / 2. Составляем и приравниваем выражения для площади:√(x^2 + 9^2) * 20 = (9 +√(20^2 - x^2)) * x
 Как икс нашли
раскрываем скобки, возводим обе части в квадрат
400 (x^2 + 81) = 81 x^2 + 18 x^2 sqrt(20^2 - x^2) + 400x^2 - x^4
400 x^2 - 81 x^2 - 400 x^2 + x^4 + 32400 = 18 x^2 sqrt(20^2 - x^2)
x^4 - 81 x^2 + 32400 = 18 x^2 sqrt(20^2 - x^2)
Снова возводим в квадрат
x^8 - 162*x^6 + 71361*x^4 - 5248800*x^2 + 1049760000 =129600*x^4 - 324* x^6
x^8 + 162 x^6 - 58239 x^4 - 5248800 x^2 + 1049760000 = 0
(x^4 + 81*x^2 - 32400)^2 = 0
Теперь уже решается биквадратное уравнение
t^2 + 81 t - 32400 = 0
t1,2 = (-81 +- sqrt(6561 + 4*32400))/2 = (-81 + - 369)/2
Отрицательный корень отбрасываем
t = 144
x = +- 12 Отрицательный корень снова не нужен

 x = 12
AB =2x=24

Хорда, перпендикулярная диаметру, делит его на отрезки 5 см и 45 см. Найдите длину хорды

Диаметр=50, радиус, следовательно, равен 25. Из центра к хорда проводим радиус,
 один катет равен 20,

 по теореме Пифагора получаем, что половина хорды равна 15, следовательно вся хорда равна 30

есть теорема, что если две хорды пересекаются, то произведение отрезков одной хорды, равно произведению отрезков другой хорды.
Получаем, что произведение отрезков искомой хорды равно 45*5=225 см
А также есть свойство, что если диметр перпендикулярен хорде, то он делит ее пополам. Значит эта хорда разделена на равные отрезки, произведение которых равно 225.
Тогда длина одного отрезка получается √225=15
Тогда длина хорды равна 15*2=30 см.

 

Радиус OB окружности с центром в точке О пересекает хорду MN в ее середине - точке К. Найдите длину хорды MN, если КВ = 1см, а радиус окружности равен 13см.

Есть такая теорема: диаметр, перпендикулярный хорде, делит ее пополам. В нашем случае радиус делит хорду пополам, а значит, он ей перпендикулярен!
OK=OB-KB=13-1=12
В треугольнике OMК OM=13, OK=12
по теореме Пифагора
\( MK=\sqrt{OM^2-OK^2}=\sqrt{169-144}=5 \)
Значит, MK=5, тогда MN=2MK=10.
Ответ: 10

1) OB=MO=OK=13см как радиусы окружности
2) ОК =OB-KB=13-1=12
3) Рассмотрим треугольник МОК, Он прямоугольный по условию (Угол ОКМ=90°)
4) MB^2=OM^2-OK^2=169-144=25
MB=5
5) Т. К. МВ=BN, то MN=5+5=10

Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 8, а расстояние от центра окружности до хорд AB и CD равны соответственно 3 и 4.

Соединяем концы хорды АВ с центром О, треугольник АОВ равнобедренный АО=ВО=радиус, проводим высоту ОН на АВ, высота=медиане АН=ВН=АВ/2=8/2=4, ОН=3, Треугольник АНО прямоугольный, АО =радиусу = гипотенузе=корень(АН в квадрате + ОН в квадрате)=
=корень (16+9) =5, радиус=5
соединяем концы хорды СД с центром О, треугольник СОД равнобедренный, проводим высоту=медиане ОМ на СД, СМ=МД, ОМ=4, треугольник ОСМ прямоугольный СМ катет=
=корень(ОС (радиус) в квадрате - ОМ в квадрате) = корень (25-16)=3
СД=2 х СМ=2 х 3 =6

К окружности с радиусом 7,5 см проведены диаметр AC и хорда AK, равная 9 см. Найдите длину хорды CK.

Решение:
1) Диаметр равен двум радиусам, следовательно он равен 15 см. (7,5*2)
2) Проведенные хорды АК и СК исходят из концов диаметра и соединяются в точке окружности, что говорит о том, что хорды друг другу перпендикулярны и образуют вписанный угол в 90° (по 2-ому следствию вписанных углов).
3) Рассмотрим треугольник АСК (прямоугольный)
АС²=АК²+СК² (теорема Пифагора)
СК²=225-81=144
СК=12
Ответ: СК=12 см.

Отрезки АВ и CD являются хордами окр-ти. Найдите длину хорды CD, если АВ=10, а расстояние от центра окр-ти до хорды АВ и СD равны соответственно 12 и 5 см

ОМ-расстояние от центра окр-ти до хорды АВ, ОN-до хорды CD.
треугольник АВО-равнобедренный, т.к. AO=OC- радиусы, значит, АМ=5,
треугольник АМО-прямоугольный, по теореме Пифагора АО=13,
треугольник OCD тоже равнобедренный, где OD=13, т.к. Это радиусы,
в прямоугольном треугольнике OND ND=12(по теореме Пифагора),
CN=ND=12, значит, CD=12*2=24

Найдите длину хорды окружности радиусом 13 см если расстояние от центра окружности до хорды равно 5 см.

АВ - хорда, О - центр окружности, ОН - расстояние от центра до хорды.  
Расстояние от точки до прямой - это длина перпендикуляра, провененного из этой точки на прямую, значит ОН - высота треугольника АОВ.
Тр-ник АОВ равнобедренный, АО = ОВ как радиусы окружности, АВ - основание. В равнобедренном тр-ке высота, проведенная к основанию, является также медианой, значит АН = ВН.
Так как ВН - высота, то тр-ник АНО прямоугольный. По теореме Пифарора найдем катет АН:
АН = √(13² - 5²) = √(169 - 25) = √144 = 12 (см)
АВ = 12 * 2 = 24(см)
Ответ: 24 см

Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=18, а расстояния от центра окружности до хорд AB и CD равны соответственно 12 и 9

Сделаем рисунок.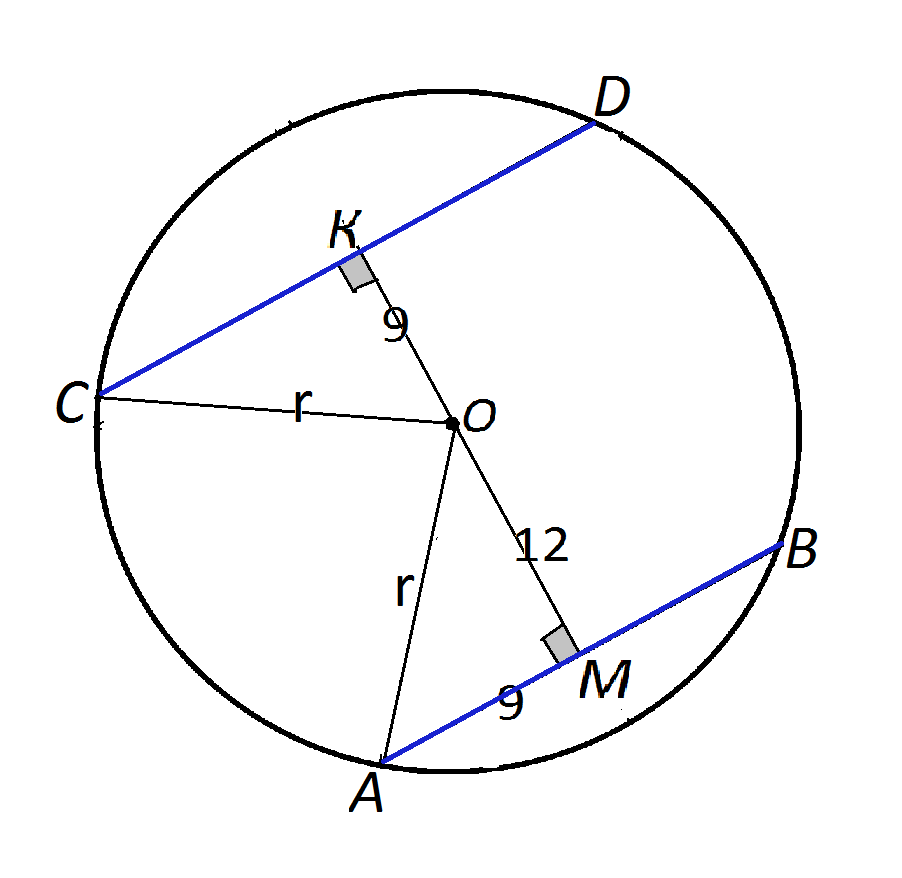  
Можно хорды нарисовать параллельными, т.к.  расстояние от центра окружности до хорд и радиус заданы условием, поэтому, поэтому  длина хорд  не меняется от места их расположения.  
Расстояние от точки до прямой измеряют отрезком, перпендикулярным к ней.   ⇒
 углы СКО и АМО - прямые, а треугольники СКО и АМО - прямоугольные.  Радиус окружности  является их гипотенузой, а половина АВ=9. 
Из треугольника АМО найдем радиус r. 
Треугольник - египетский, т.к. Отношение катетов 3:4, следовательно, радус равен 15 ( можно проверить по т. Пифагора). 
Треугольники СКО и АМО равны по гипотенузе и меньшему катету, из чего следует, что больший катет второго треугольника равен 12. 
СD=2 СК=24. 
-
bzs*

Найдите длину хорды АВ, находящейся на расстоянии 9 от центра окружности О, если радиус окружности ОА = 15.

Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.  
Диаметр-тоже хорда, наибольшая по длине.
Хорда АВ перпендикулярна диаметру.
Хорда АВ делит диаметр на 2 части: 15+9=24 и 15-9=6
Хорда АВ делится диаметром на 2 равные части: х и х.
х*х=24*6
х^2=144
х=12
длина хорды равна 12+12=24

Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=40, а расстояния от центра окружности до хорды AB и CD равны соответственно 21 и 20

Рассмотрим равнобедренный ΔАОВ (ОА=ОВ как радиусы). Расстояние от О до АВ - это высота ОН=21 треугольника АОВ (она же и медиана, и биссектриса). Значит можно по т. Пифагора найти радиус ОА:
ОА²=ОН²+(АВ/2)²=21²+20²=841
Аналогично равнобедренный ΔСОД (ОС=ОД радиусы). Расстояние от О до СД- это высота ОМ=20 треугольника СОД (она же и медиана, и биссектриса). Значит можно по т. Пифагора найти СД:
(СД/2)²=ОС²-ОМ²=841-20²=441
СД/2=21
СД=42