Двугранный угол при основании правильной четырехугольной пирамиды равен α. Высота пирамиды равна H. Найдите объем конуса, вписанного в пирамиду.

Решение:
Высота конуса совпадает с высотой пирамиды. Радиус основания конуса отметим за у, а образующая  = х (так как двугранный угол равен а, т.е угол между образующей и основанием) по прямоугольному треугольнику в сечении конуса найдем: sin A= H/X x = H/sinA, a cosA = y/x = у/H/sinA = у = ctgA*H V = s осн * H / 3 S осн = ПИ * R" = ПИ* у" = ПИ"*ctg"A*H" V = (ctg"A)*(H")*(ПИ)*(H) / 3

---

Пирамида правильная  четырехугольная - значит,  её основанием является квадрат.  
Высота конуса, вписанного  в пирамиду,  совпадает с высотой пирамиды, а радиус основания равен половине ее стороны, как радиус окружности, вписанной в квадрат.  
Объем конуса находят по формуле 
V=πr² ·h/3
 По условию h=H
r=?
Пусть высота пирамиды МО, апофема =образующей конуса = МР, радиус r основания конуса - ОР.  
r=ОР:MO=ctg α
r=H·ctg α
V=π (H·ctg α)²*H/3= πH³·ctg²α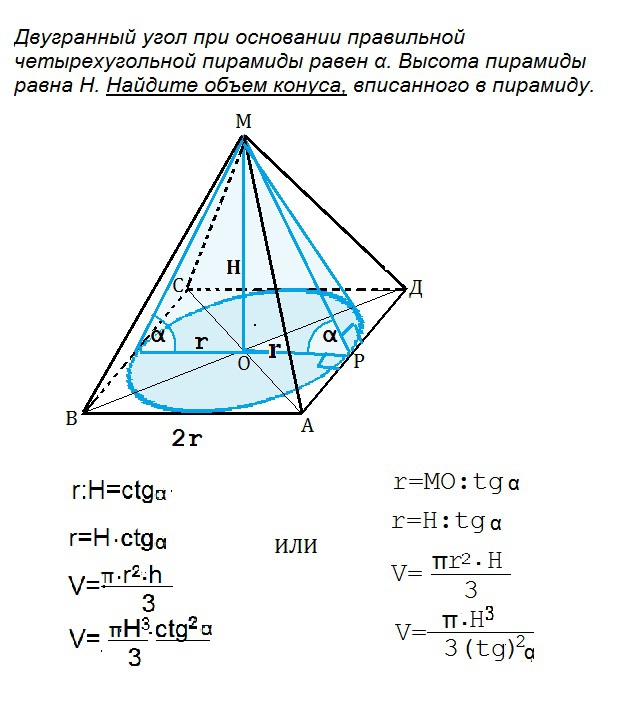