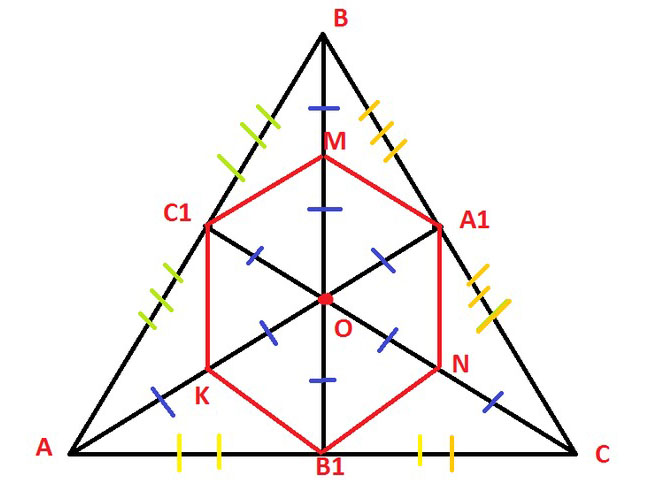
В правильном треугольнике АВС медианы АА1, ВВ1 и СС1 пересекаются в точке О. Точки K, M и N – середины отрезков АО, ВО и СО соответственно. Найти периметр шестиугольника A1MC1KB1N, если АВ = a.

Решение:

В правильном треугольнике высоты, биссектрисы и медианы, опущенные из одной вершины совпадают и равны между собой, то есть АА1=ВВ1=СС1
Медианы точкой пересечения делятся в отношении 2:1 ⇒ ВО=АО=СО=2х, ОА1=ОВ1=ОС1=х;
По условию K, M и N – середины отрезков АО, ВО и СО соответственно ⇒
МО=КО=NO=АО/2=2х/2=х ⇒МО=КО=NO=ОА1=ОВ1=ОС1=х ⇒A1MC1KB1N=правильный шестиугольник
В равностороннем треугольнике высота=а√3/2
BB1=BO+OB1=2x+x=3x
BB1=а√3/2
а√3/2=3x
x=а√3/6
OB1=x
OC=2x
B1C²=OC²-OB1²=4x²-x²=3x²
B1C=√3x²=x√3
В1N-медиана для треугольника ОСВ1
В1N²=(2( ОВ1²+В1С²)-ОС²)/4=( 2(x²+3x²)-4x² )/4=(8x²-4x²)/4=4x²/4=x²
В1N√x²=x=а√3/6
P=6x=6*а√3/6=a√3
отв: a√3