Около окружности, радиус которой равен 4, описан многоугольник, периметр которого равен 51. Найдите его площадь

Решение:

S =S(A₁OA₂)+S(A₂OA₃)+.+S(AnOA₁) = A₁A₂*r/2+A₂A₃*r/2+.+AnA₁*r/2 = 
r(A₁A₂*+A₂A₃+.+AnA₁)/2*=(P/2)*r =(51/2)*4 =51*2 =102
* * * A₁A₂; A₂A₃;.AnA₁ стороны многоугольника, O_ центр окружности, 
r  _ радиус  окружности   * * *
* * * * * * * * * * * * * * * * * * * *
S=(a₁*r)/2 +(a₂*r)/2 +. +(an*r)/2 = r*(a₁ +a₂ +. +an)/2 =(P/2)*r.

Если соединить центр окружности с вершинами многоугольника, получим треугольники, сумма сторон которого, расположенных вне окружности, периметр описанного многоугольника.  
Проведем из центра ( общей вершины каждого получившегося треугольника) высоты к сторонам многоугольника.
т.к. Площадь треугольника находят по формуле 
   S=a*h:2,
а высота здесь равна радиусу, проведенному в точку касание окружности со стороной каждого треугольника, ⇒ 
 S=a*r:2
Площадь многоугольника равна сумме площадей всех этих треугольников с вершиной в центре вписанной в него окружности.  
S=а₁*r:2+ a₂*r:2+a(n)*r:2=r*(a₁+a₂+a₃+a(n)):2=r*P:2=r*p ⇒ 
Площадь многоугольника равна произведению его полупериметра и радиуса окружности, вписанной в этот многоугольник. ( верно, естественно, и для треугольника с вписанной в него окружностью)
S=51*4:2=102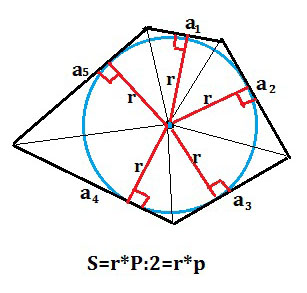