В выпуклом многоугольнике число диагоналей, исходящих из вершины, равно 15. Найти число всех диагоналей этого многоугольника.

Решение:

Из одной вершины можно провести диагонали ко всем вершинам, кроме себя и двух соседних. Т.е. число диагоналей из одной вершины на 3 меньше числа вершин многоугольника.
Значит, у заданного многоугольника 15+3=18 вершин.
Всего диагоналей будет число вершин умножить на к-во диагоналей из одной вершины, деленное пополам, т.к. Каждая диагональ при этом считается 2 раза.
18*15/2 = 9*15 = 135

---

Чтобы решить задачу, для начала выясним количество углов в выпуклом многоугольнике.
т.к. из одной вершины исходит 15 диагоналей значит напротив этой вершины находится 15 других вершин и ещё две (смотри рисунок во вложении) т.е. Всего 15+2+1=18 вершин (15 напротив, 2 по бокам и 1 вершина из которой выходят диагонали)
далее количество диагоналей выпуклого n-угольника вычисляется по формуле K=n(n-3)/2=18(18-3)/2=18*15/2=270/2=135
Ответ: 135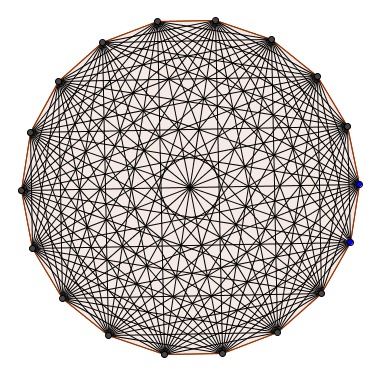