Окружность разделена точками на четыре части, градусные величины которых относятся как 3 : 7 : 5 : 3. Найдите углы многоугольника, полученного последовательным соединением точек деления.

Решение:

Пусть коэф. Пропорц. Равен х. Тогда углы равны 3х, 7х, 5х, 3х. 3х+7х+5х+3х = 360. 18х=360; х=20. Тогда углы равны 3*20=60 гр; х, 7*20=140 гр;, 5*20=100 гр;, 33*20=60 гр; Тогда найдём углы при сторонах многоугольника: из 1 треугольника (180-60):2=60 (град); из 2 треугольника (180-140):2=20 (град); из 3 треугольника (180-100):2=40 (град); из 4 треугольника (180-60):2=60 (град); Тогда углы многоугольника будут равняться: 1) 60 + 20 = 80 (град); 2) 40 + 20 = 60 (град); 3) 60 + 40 = 100 (град); 4) 60 + 60 = 120 (град). Ответ: 80 (град); 60 (град); 100 (град); 120 (град).

---

Величина углов четырехугольника равна половине градусной меры центральных углов, на которые опираются, как вписанные, углы этого четырехугольника.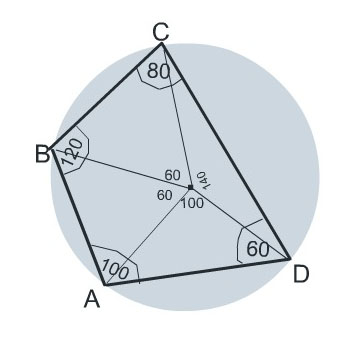
Окружность делится на дуги, отношение которых 3:7:5:3, и коэффициент этого отношения равен (3+7+5+3)=18
360:18=20ᵒ.
Получившиеся дуги, на которые опираются центральные углы, равны соответственно:
3·20=60ᵒ
7·20=140ᵒ
5·20=100ᵒ
3·20=60ᵒ
-
Вписанные в окружность углы равны:
∠ А опирается на дугу центрального угла ВС+СD=140+60=200ᵒ и равен 100ᵒ
∠ В опирается на дугу центрального угла CD+AD=100+140= 240ᵒ и равен 120ᵒ
∠ С - опирается на дугу центрального угла AB+AD=160ᵒ и равен 80ᵒ
∠ D - опирается на дугу центрального угла AB+BC=120ᵒ и равен 60ᵒ