| Главная Научный калькулятор | |
|
|
Постройте треугольник по двум сторонам и медиане, проведенной к одной из них.Решение: Сначала построим любую из сторон. Найдём ее середину. Пусть это точка О. Через эту точку проведём окружность радиусом равным длине медианы. Затем радиусом равным длине второй стороны и с центром в одной из конечных точек постороеной стороны тоже проведём окружность. Точка пересечения этих окружностей и будет третьей вершиной треугольника. 1) Проведём прямую а и отметим на ней точки А и В - концы отрезка 2) С помощью циркуля разделим этот отрезок пополам (Вы умеете находить середину отрезка с помощью 2х засечек с разных концов отрезка?). И отметим центр стороны D. 3) С помощью циркуля радиусом, равным длине медианы из точки D сделаем засечку в районе предполагаемой третьей вершины треугольника 4) Такую же засечку делаем радиусом, равным стороне ВС из точки В, место пересечения дуг даст нам вершину С. 5) Соединим точки В и С, а также А и С - получаем искомый треугольник. 1. Начертите одну известную сторону, найдите в ней середину с помощью линейки (это точка в которую приходит медиана), потом возьмите циркуль и задайте ему раствор размером с медиану, потом поставьте иголку циркуля в середину отрезка и отчертите полуокружность. Далее возьмите раствор циркуля размером со вторую сторону треугольника, поставьте иголку циркуля на конец первого отрезка и отчертите полуокружность так, чтоб она пересеклась с первой полуокружностью. Точка пересечения - это вершина треугольника. Соедините линейкой концы первого отрезка с этой точкой. Пусть две стороны будут а и b, а медиана — m. Построим треугольник по трем сторонам: АВ = а, BD = b, AD = 2m; Проведем медиану ВА1 и на ее продолжении отложим А1С = А1В; Проведем сторону АС. ΔАВС — искомый. Докажем это:ΔBA1D = ΔCA1A (по 1-му признаку равенства треугольников). Таким образом, АС = BD = bAB = aAA1 = AD = 2m : 2 = m АА1 — медиана. 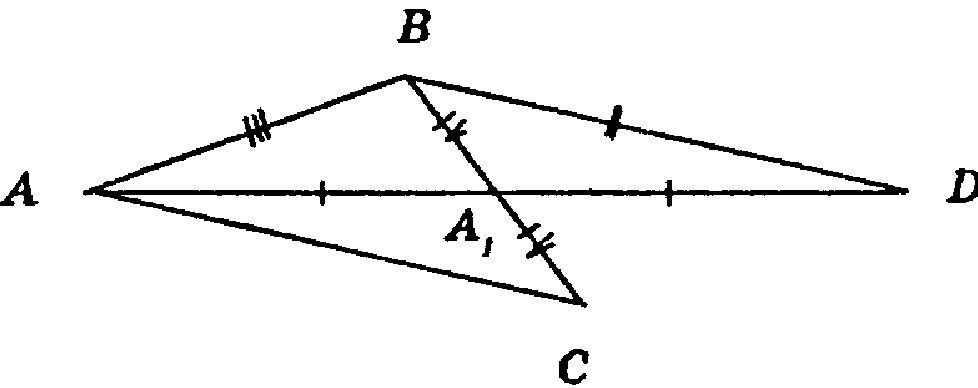 |