Дан отрезок длиной 1. С помощью циркуля и линейки построить отрезок длиной корень 5

Решение:

Отложим отрезок длиной 1

к его концу отложим перпендикуляр длиной 1

Соединив эти два отрезка получим отрезок длиной корень с 2

К последнему отрезку построим перпендикуляр длиной 1

И соединим два последних отрезка итоговый будет длиной корень с 3

Потом опять к последнему отрезку проведем перпендикулярный отрезок длиной 1. Соединим концы двух последних отрезков, получим отрезок длиной корень с 4

И еще раз к последнему отрезку к концу проведем перпендикуляр и соединим последние два отрезка - это и будет отрезок длиной корень 5

Построить отрезок длиной √(a² - b² - ab) где a>b, a и b - длины двух данных отрезков

Построить отрезок x = √(a² + b² - ab) не составляет труда. Это третья сторона в треугольнике, где между a и b 60 градусов. Построить 2 луча под углом 60 градусов вы должны уметь (проще всего просто построить равносторонний треугольник и воспользоваться 2 его сторонами, вдоль них отложить a и b, и соединить концы.

Теперь надо еще построить отрезок длины y =b*√2. Это - диагональ у квадрата со стороной b. Это тоже можно сделать циркулем и линейкой.  

Вот теперь, имея 2 отрезка - x = √(a² + b² - ab) и y = b*√2, считаем первый гипотенузой в прямоугольном треугольнике, а второй - катетом. Строим треугольник (это учебная задача, тут на сайте её 1000 раз решали, если сами не можете) по гипотенузе x и катету y, второй катет как раз и равен √(a² - b² - ab);

Построить отрезок длиной √(a² + b² + ab)

1) Берём прямую через точку A

2) В точке A строим угол с прямой в $60^0$ (Ну, как строить равносторонние треугольники c помощью циркуля думаю, что знаете). 

3) На втором луче из точки A отмечаем отрезок AB длиной a

4) Из точки B на исходную прямую опускаем перпендикуляр BC. Соответственно $|AC|=\frac{1}{2}\cdot|AB|=\frac{a}{2}$, так как катет против угла в $30^0$

$|BC|=\sqrt{|AB|^2-|AC|^2}=\sqrt{a^2-(\frac{a}{2})^2}=\frac{a\sqrt{3}}{2}$

5) От точки A в сторону от точки C отмеряем отрезки длиной b. Получаем отрезок CD, где  $|CD|=\frac{a}{2}+b$.

6) Вычислим длину отрезка BD.

$|BD|=\sqrt{|BC|^2+|CD|^2}=\sqrt{(\frac{a\sqrt{3}}{2})^2+(\frac{a}{2}+b)^2}$

$|BD|=\sqrt{\frac{3a^2}{4}+\frac{a^2}{4}+2\frac{a}{2}b+b^2}=\sqrt{a^2+ab+b^2}$

Итог - отрезок BD будет иметь требуемую длину.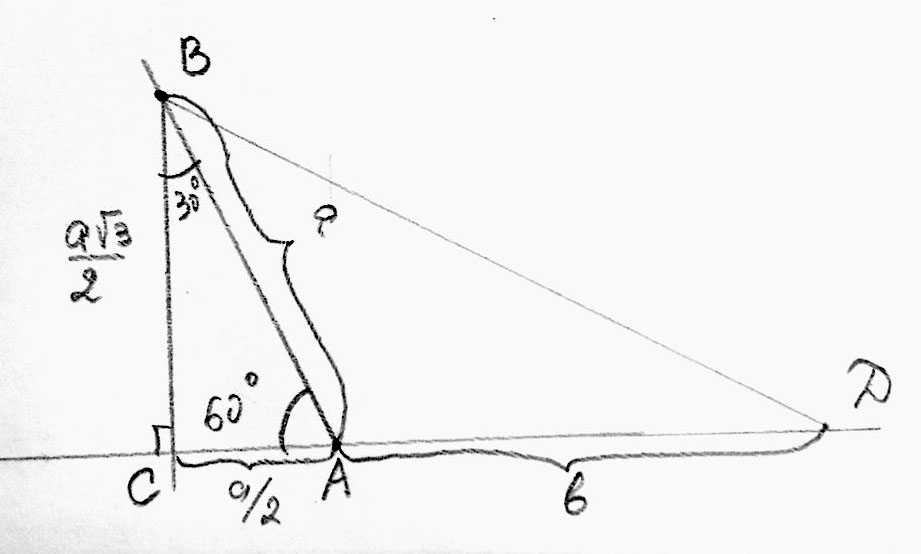