Дан шестиугольник А1А2А3А4А5А6. Его стороны А1А2и А4А5, А2А3и А5А6, А3А4и А6А1попарно равны и параллельны. Используя центральную симметрию, докажите, что диагонали А1А4, А2А5, А3А6данного шестиугольника пересекаются в одной точке.

Решение:

Нужно рассмотреть фигуры: А1А3А4А6, А2А3А5А6, А3А4А6А1. Так как по условию стороны. Попарно равны и параллельны, то эти фигуры будут параллелограммами! У них диагонали точкой пересечения (предположим О) делятся пополам. Рассмотрим А1А3А4А6 у него А1О=А4О=А1А4/2 также  А3О=А6О=А3А6/2.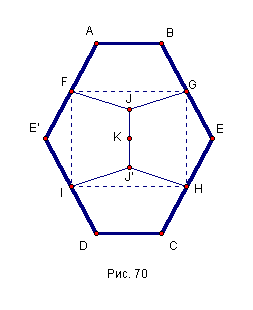
Теперь рассмотрим А2А3А5А6 пусть у него диагонали пересекаются в О1. Тогда А2О1=А5О1=А2А5/2 также А3О1=А6О1=А3А6/2. 
Смотрим на последние равенства: А3О=А6О=А3А6/2 и А3О1=А6О1=А3А6/2 и точка О и О1 находятся посередине А3А6 а значит они совпадают.  
Всего проведено три диагонали, две из них пересекаются в одной точке, а третья тоже проходит через эту точку по нашему доказательству.
Лучше такой рисунок сделать (обозначение и центральную часть сделать по условию задачи)