Ребро куба ABCDA1B1C1D1 равно a. Постройте сечение куба, проходящее через прямую B1C и середину ребра AD, и найдите площадь этого сечения.

Решение:
Через 3 точки можно провести плоскость, и только одну.
Стороны сечения куба этой плоскостью будут лежать на гранях куба.  
Данное сечение куба - трапеция КЕВ1С  
с большим основанием В1С и
 меньшим ЕК.  
В1С= диагональ грани и равна а√2 по свойству диагонали квадрата.
ЕК=(а/2)√2 на том же основании
КС²=ДС²+КД²=а²+ 0,25а²=1,25а² 
Проведем высоту КН трапеции.
 Высота равнобедренной трапеции из тупого угла делит большее основание на отрезки, равные полуразности и полусумме оснований.  
НС=(В1С-КЕ):2=(а√2-0,5а√2):2=0,25а√2
КН²=КС² - НС²=1,25а²-(0,25а√2)²=1,25а²-0,125а²=1,125а²

КН=√(1,125а²)=1,5а√0,5 
Площадь трапеции равна произведению высоты на полусумму оснований:
S=KH*(EK+B1C):2=
=1,5а√0,5*(0,5а√2+а√2):2=
=(1,5а√0,5)*0,75а√2=
=1,5а*0,75а*√(0,5*2)=1,125а²
-
Для нахождения площади трапеции существует не только та  формула, которую в большей части случаев мы используем.  
В приложенном рисунке дана формула для произвольной трапеции и для равнобедренной трапеции через стороны.
По ней площадь получается та же,  что по обычной формуле через назождение высоты.
S=1,125а²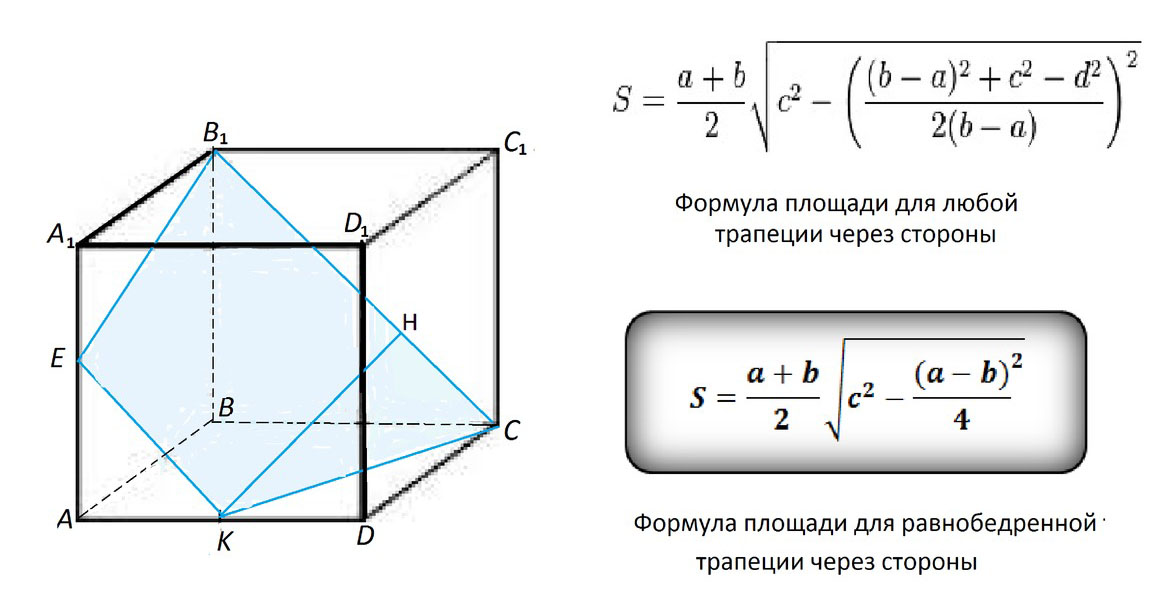