Главная       Научный калькулятор
Меню


Построить прямоугольный треугольник по гипотенузе и острому углу



Решение:

На одной из сторон угла отмеряем гипотенузу. Пусть это точки С (угол) и А.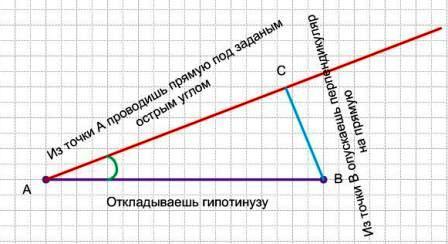
АС - гипотенуза. Из точки А циркулем на продолжении второй стороны угла
Делаем засечку длиной гипотенузы, получаем точку Д. Теперь из точек Д и С делаем засечки равные гипотенузе на противоположной от точки А стороне.
Получим точку Е. Соединяем точки Е и А. Пересечение со стороной угла и даст третью точку треугольника.

Свойство прямоугольного треугольника: гипотенуза - это диаметр окружности, на которой будет лежать вершина прямого угла

ПОСТРОЕНИЕ

- проводим гипотенузу АВ (дана по условию)

- строим окружность

- откладываем транспортиром острый угол АВК (дан по условию) от любой конца  гипотенузы 

- сторона этого угла ВК пересекает окружность в точке С 

точка С - это вершина прямого угла треугольника

- соединяем точки С и А

треугольник построен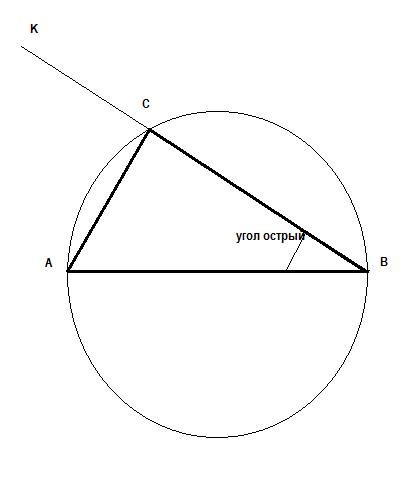

Берем угол. Вершина угла - точка А. На одном из лучей откладываем длину гипотенузы. Получаем точку В. А затем из точки В опускаем перпендикуляр на другой луч. Получаем точку С - вершину прямого угла. Чтобы опустить перпендикуляр из точки (номер 1, в нашем случае - это точка B) на прямую, надо поставить острие циркуля в эту точку и произвольным одинаковым раствором циркуля (явно большим расстояния от точки до прямой) сделать две засечки на этой прямой, получим две точки пересечения (номер 2 и номер 3), а затем, ставя поочередно в эти точки острие циркуля одинаковым раствором циркуля (не обязательно равным первоначальному, но явно большему половины длины отрезка между точками 2 и 3, а лучше просто не менять раствор циркуля) провести две дуги до их пересечения на другой стороне прямой (а если поменять раствор циркуля, то можно провести две дуги до пересечения и на той же стороне прямой, где была точка номер 1). Получим четвертую точку - точку пересечения дуг. Соединим первую точку с четвертой до пересечения с прямой, если они по разные стороны от прямой, или продлим линию до пересечения с прямой, если точки 1 и 4 находятся по одну сторону от прямой. Эта линия и будет перпендикуляром, опущенным из первой точки на данную прямую. А точка пересечения перпендикуляра с прямой и будет точкой С нашего треугольника.

Дано:

угол АВС (острый) и угол АСВ (прямой), отрезок АВ (гипотенуза)

1) начертим луч а. Отрезок МК=АВ (чертим с помощью циркуля)

2) построим угол РМК = углу АВС (тоже с помощью циркуля и линейки)

3) МР = АВ (построить луч)

4) построим прямой угол РКМ

5) соединяем между собой все элементы.

В решении это надо записать так:

1) луч  а. МК=АВ

2) угол РМК=углу АВС. (далее надо описать (тоже пошагово) как строили угол РМК, равный углу АВС.

3) луч  МТ, МР = АВ

4) угол РКМ = 90 \( а \)  

5) луч КS

6) луч МТ пересекается с лучом КS в точке Р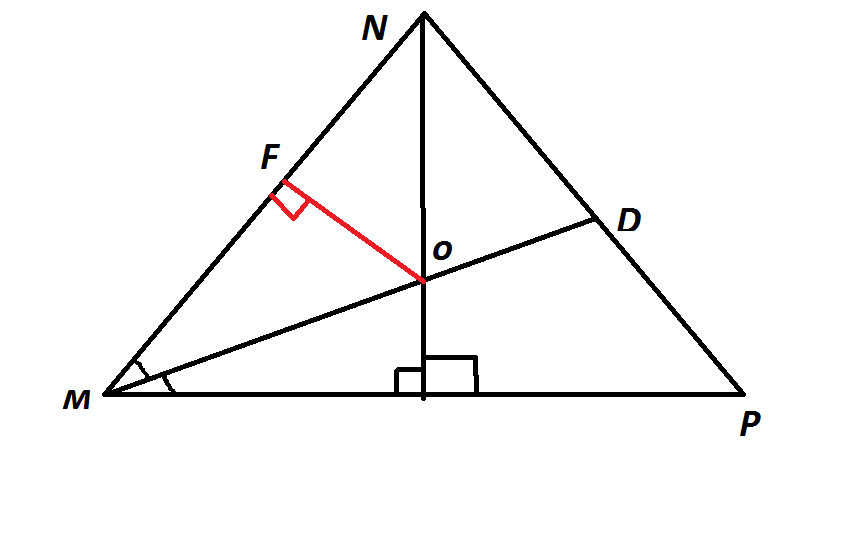

Сначала нужно найти 2 острый угол, строим произвольный прямоугольный угол, на одном из его лучей ставим произвольно точку, отмечаем данный нам по условию угол и получаем второй острый. Дальше строим данную гипотенузу и отмечаем относительно неё два острых угла.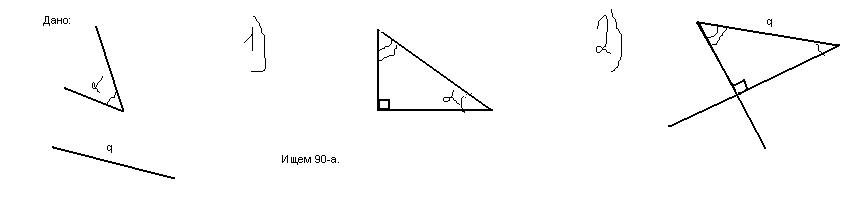

Рисуешь некоторый угол, к примеру φ, расположенный между прямыми а и б,  любым раствором циркуля проводишь окружность с центром в точке φ. Далее рисуешь прямую ц, на ней берёшь произвольную точку, к примеру A. Это точка и будет одной из вершин треугольника. Из точки А строим точно такой же угол φ с помощью простых действий: из точки А проводишь окружность с тем же раствором циркуля как и поступили с углом φ, эта окружность пересекается с прямой в двух точках M и N, нам нужна лишь одна, к примеру M,  между прямыми а и б замеряем с помощью циркуля и с этим радиусом проводим окружность из точки M, на пересечении двух окружностей появятся две точке, там нужна лишь одна, будем называть её E, через точки А и E проводишь прямую. Далее строишь перпендекуляр в произвольной точке B на прямой ц следующим образом: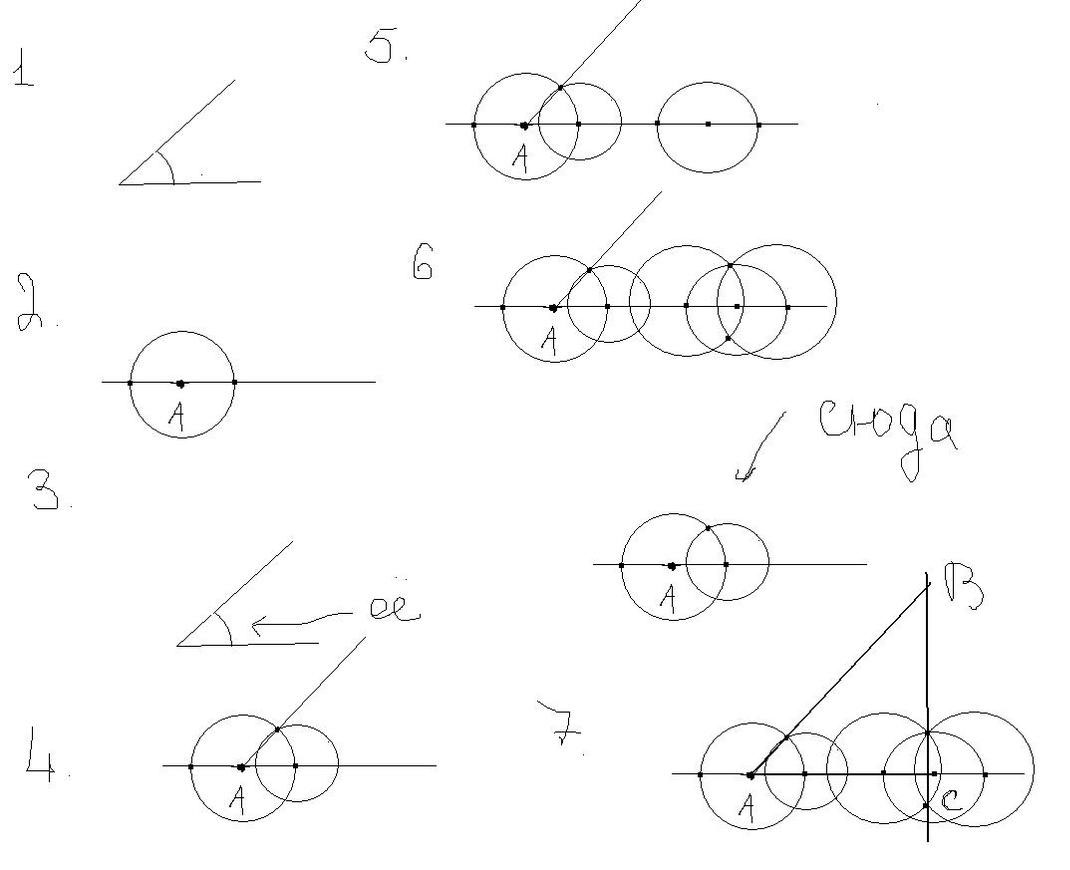
проводим окружность любым раствором циркуля из взятой точке B, появились две точки, из каждой точки проводим ещё по окружности раствором больше, чем мы брали для получения этих. Через 2 точки пересечения проводим прямую - она и будет перпендекуляром. На пересечении полученных прямых появилась ещё одна точка, которая будет заключающейся точкой C. Мы получили треугольник ABC
1) строим окружность 1 с центром в точке L произвольного радиуса
2) Отмечаем т. Пересечения окружности 1 со сторонами угла KLM - т. K’ и L’
3) строим окр. С центром 2 в т. А тем же раствором
4) отмечаем т. Б’ пересеченмя окружности с лучём [AB).
5) проведём окружность 3 с центровм в т. B’ радиуса K’L’
6)отметили т. C пересечения окружности 2 и окружности 3
7) строим луч [AC)
8) строим окружность 4 с центровм в т. Б лежащий на прямой а, ридиус произвольный но, > либо = 1/2 |АB|
9) K1,L1 точки пересечения окружности 3 и окружности 4
10) K1L1 -искомый перпендекуляр
11) треугольник ABC -искомый