Найдите площадь правильного шестиугольника, если его сторона равна 9.

Решение:

R=а6=9 см - радиус описанной окружности

r=R*cos(180/n)=9*cos30=4,5√3 см - радиус вписанной окружности

S=0.5Pr=0.5*54*4,5√3=121,5√3 см кв - площадь шестиугольника (Р=6а=54)

правильный шестиугольник состоит из 6-ти правильных треугоьников, сторона каждого трегольника равна стороне 6-тиугольника

площадь правильно треугольника

S=V3*a*а/4

площадь правильного 6-тиугольника

S=6*V3*a*а/4=6*9*9V3/4=121,5V3 

V-корень квадратный 

Найдите площадь правильного восьмиугольника, если площадь кругового сектора, соответствующего центральному углу восьмиугольника, равна 2π

Площадь сектора выражена формулой
S=а πR²:360°, где а - центральный угол сектора

Угол при центре окружности у этого сектора равен 360:8=45°
45°πR²:360°=2π
45°R²:360°=2
45°R²=2∙ 360°
R²=720:45
R²=16см²
R=4 см
Высота каждого из 8 треугольников, составляющих поверхность правильного восьмиугольника, проведенная из угла к радиусу окружности, является стороной равнобедренного прямоугольного треугольника с гипотенузой, равной радиусу.

Найдем эту высоту по формуле диагонали квадрата, т.к. Этот треугольник- половина квадрата.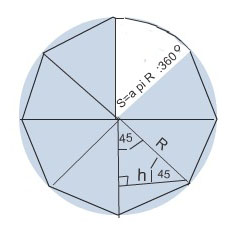
d=a√2, где а - сторона этого треугольника, а d - гипотенуза, и равна она радиусу окружности R=4.
4=а√2
а=4:√2= 2√2см
Найдем площадь одного треугольника из восьми
S=( 4∙2√2):2=4√2 см²
Площадь восьми таких треугольников равна
S=8∙4√2=32√2см²

Найдите площадь правильного многоугольника, если его внешний угол равен 30°, а диаметр описанной около него окружности равен 8 см.

Очень легко показать, что внешний угол в правильном многоугольнике равен центральному углу в описанной окружности, опирающемуся на сторону. В самом деле, угол многоугольника равен 180 - Ф, если провести из центра радиусы в соседние вершины, то угол при основании в полученном равнобедренном треугольнике равен (180 - Ф)/2, сумма 2 углов при основании 180 - Ф, поэтому угол при вершине Ф.  

Поскольку при Ф = 30 градусов число сторон N = 360/Ф = 12, то у в задаче задан правильный 12-угольник. Радиуc описанной окружности R = 4, и площадь каждого из 12 уже упоминавшихся треугольников равна R^2*sin(30)/2 = 4; площадь всего 12-угольника 4*12 = 48;

Найдите площадь правильного восьмиугольника с стороной а=3(корень под корнем корень из 2 -1) сантиметров

1. Найти центральный угол каждого треугольника, из которых состоит восьмиугольник
360:8=45°
2. Н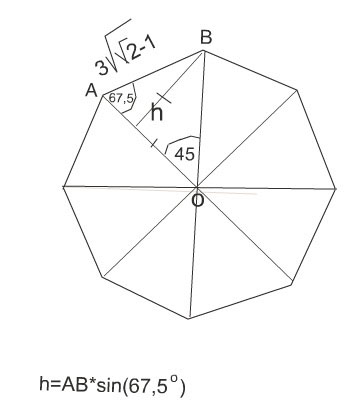айти угол равнобедренного треугольника при основании=стороне восьмиугольника
(180-45):2=67,5°
3. Найти высоту треугольника АОВ
h=AB*sin (67,5)
Так как угол АОВ=45°, то
АО=ВО=h√2

S АОВ=h*АО:2
Площадь восьмиугольника равна 8*S АОВ

-

Вычислите площадь правильного шестиугольника

Пусть нам известна хотя бы сторона этого шестиугольника). Пусть она равна а. Кстати, радиус описанной окружности тоже равен а. Этот шестиугольник состоит из 6 равных треугольников. Достаточно вычислить площадь хотя бы одного. Треугольники будут равносторонними. Потому что угол при вершине треугольника, где центр этого шестиугольника, равен 360:6=60. А другие два угла равны между собой как в равнобедренном треугольнике. Значит 180-60=120 градусов - сумма двух одинаковых углов треугольника. 120:2=60 градусов - мера углов при основании треугольника. Площадь равностороннего треугольника со стороной а можно вычислить по формуле, перемножив две одинаковые стороны друг на друга, затем умножив на синус 60 градусов и разделить пополам.

\( S_\Delta=a*a*\sin60^0*0,5 \)

\( S_\Delta=a*a*\frac{\sqrt{3}}{2}*0,5 \)

\( S_\Delta=\frac{a^2\sqrt{3}}{4} \)

Всего таких треугольников 6. Значит надо умножить на 6.

Получается ответ

\( \frac{a^2*3\sqrt{3}}{2} \)

Площадь вписанного в круг правильного треугольника на 18,5 меньше площади вписанного в тот же круг квадрата. Найдите площадь правильного шестиугольника, вписанного в тот же круг.

Обозначим сторону треугольника а, сторону квадрата с, радиус круга R. Из свойств описанной окружности R=a/2sin60=a/3^1/2, R=2^1/2*c/2, отсюда a=R*3^1/2, c=R*2^1/2. Площадь треугольника S1=(a/2)(a3^1/2)/2=3/4*R^2*3^1/2, площадь квадрата S2=c^2=2R^2. По условию S2-S1=18,5. Подставив найденные значения площадей получим уравнение из которого находим R. Площадь вписанного шестиугольника равна S3=3/2*R^2*3^1/2

Найдите площадь правильного шестиугольника, сторона которого равна корень из 5

Площадь правильного шестиугольника равна

\( S=\frac{3a^2\sqrt{3}}{2} \)

Площадь данного шестиугольника

\( S=\frac{3*(\sqrt{5})^2*\sqrt{3}}{2}=\frac{15\sqrt{3}}{2} \)

Правильный шестиугольник состоит из 6 равных треугольников, причём треугольники - равносторонние, тогда углы треугольника =180/3= 60 град

Значит площадь одного треугольника = \( \frac{1}{2}*\sqrt{5}*\sqrt{5}* sin 60=2.5*\frac{\sqrt3}{2}=\frac{2.5\sqrt3}{2} \)

тогда S шестиугольника= \( \frac{2.5\sqrt3}{2} * 6=7,5\sqrt3 \)

Ответ площадь равна 7.5корней из3 см2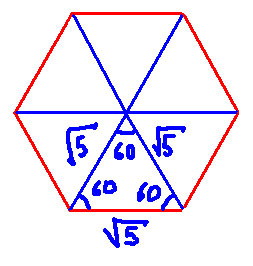

Найдите площадь правильного шестиугольника, если площадь кругового сектора, соответствующего центральному углу шестиугольника, равна 6п

Найдём градусную меру центрального угла: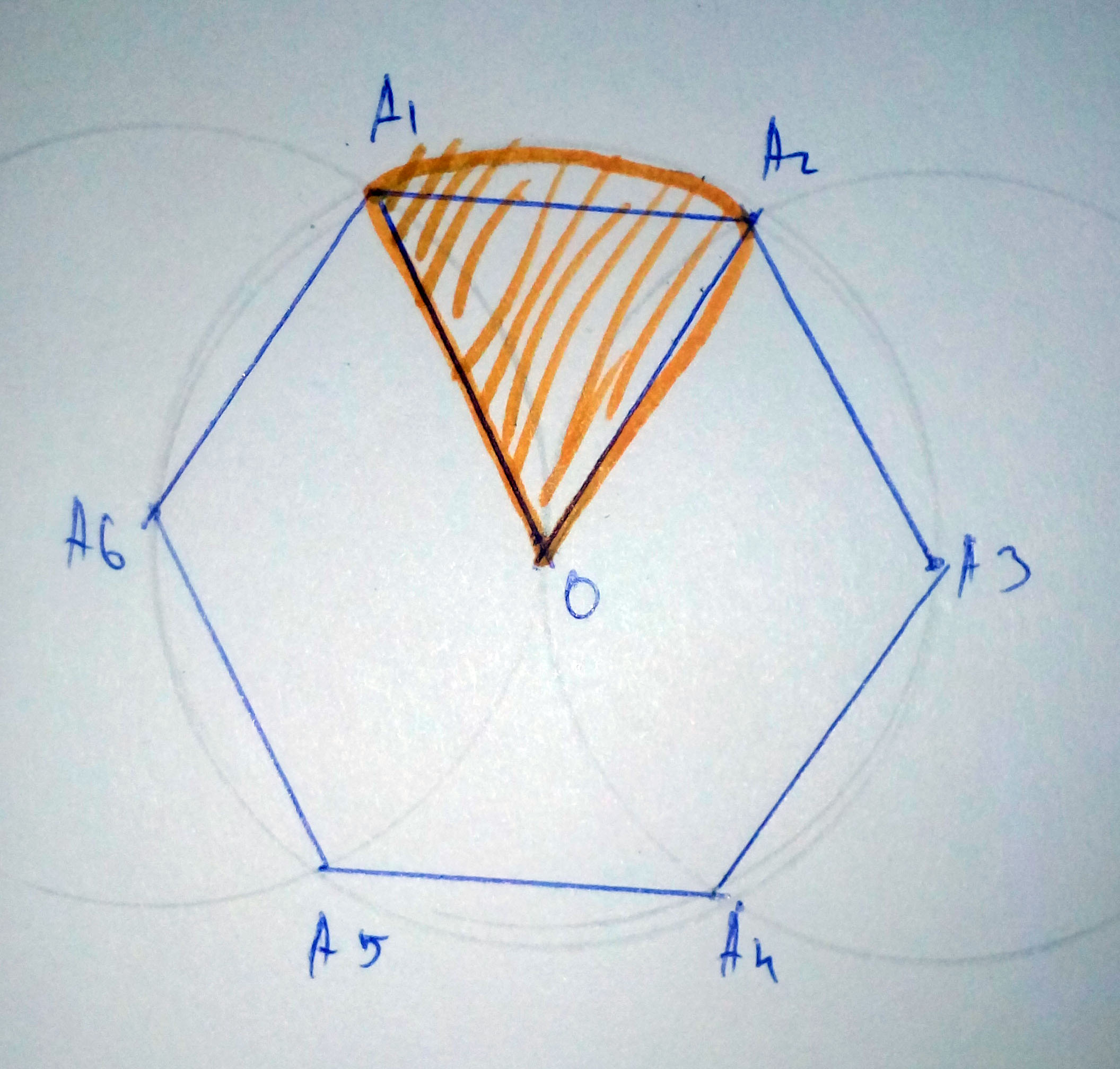
Исходя из того, что опираться он будет на дугу описанной окружности, каждый угол шестиугольника равен 120°, а радиусы являются биссектрисами его углов, получаем:
180° - 120°/2 - 120°/2 = 180° - 60° - 60° = 60°.
Площадь кругового сектора находится по формуле:
Sсек = πr²A/360°
A = 60°.
Значит, Sсек = 1/6Sокруж
Sокр. = 6Sсек = 6•6π = 36π.
Радиус описанной окружности тогда равен √Sокр/π = 6.
Радиус описанной окружности равен стороне шестиугольника.
Радиус вписанной окружности равен:
r = R√3/2 = 6√3/2 = 3√3.
Площадь любого описанного многоугольника находится по формуле:
S = 1/2Pr
Sшест. = 1/2•6a•3√3 = 1/2•6•6•3√3 = 54√3