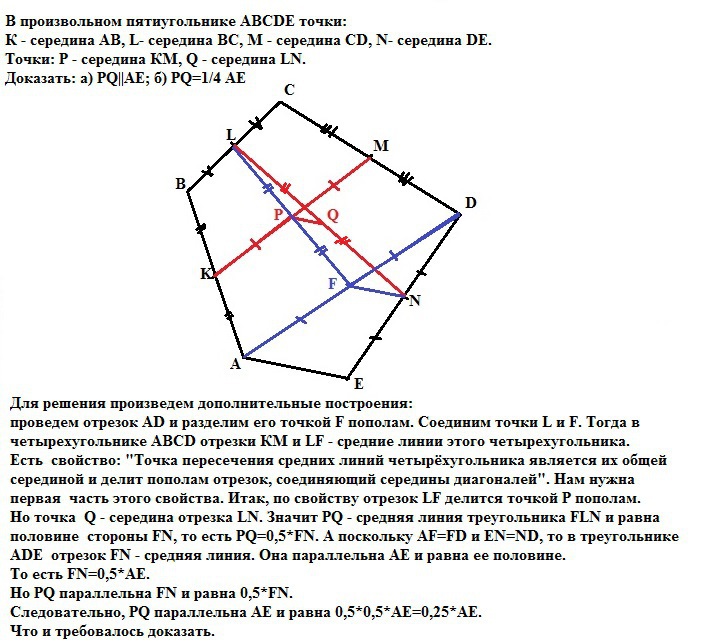
В произвольном пятиугольнике АВСDЕ точки:
К - середина АВ, L- середина ВС, М - середина СD, N- середина DЕ.
Точки: Р - середина КМ, Q - середина LN.
Доказать: а) PQ||АЕ; б) PQ=1/4 AE

Решение:

Для решения произведем дополнительные построения:
проведем отрезок АD и разделим его точкой F пополам и соединим точки L и F. Тогда в четырехугольнике АВСD отрезки КМ и LF - средние линии этого четырехугольника. Есть свойство: "Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей". Нам нужна первая часть этого свойства. Итак, по свойству отрезок LF делится точкой Р пополам. Но точка Q - середина отрезка LN.
Значит PQ - средняя линия треугольника FLN и равна половине стороны FN, то есть PQ=0,5*FN. А поскольку АF=FD и EN=ND, то в треугольнике ADE отрезок FN - средняя линия.
Она параллельна АЕ и равна ее половине. То есть FN=0,5*AE.
Но PQ параллельна FN и равна 0,5*FN.
Следовательно, PQ параллельна АЕ и равна 0,5*0,5*АЕ=0,25*АЕ.
Что и требовалось доказать.