Постройте прямоугольный треугольник по катету a и сумме s другого катета и гипотенузы.

Решение:

Чтобы построить пр. тр-к, достаточно знать длины катетов. Один известен: а. Пусть b - другой катет. С - гипотенуза

b+c=s - по условию

Тогда применв теорему Пифагора для с, получим следующее уравнение для b:

\( b+\sqrt{a^2+b^2}=s,\\ a^2+b^2=s^2-2bs+b^2 \)

\( 2bs=s^2-a^2,\\ b\ =\frac{s^2-a^2}{2s}. \)

Катет b найден и прямоугольный треугольник строится автоматически по двум перпендикулярным отрезкам а и b.

---

Пусть даны катет АС и отрезок СК, равный сумме второго катета и гипотенузы. Нужно с помощью циркуля и линейки построить прямоугольный треугольник АВС.  

1) На произвольной прямой отмечаем точку С.  

Из точки С возводим перпендикуляр. Для этого по обе стороны от С отмечаем точки 1 и 2 и из них, как из центра, проводим полуокружности по обе стороны от С. Точки пересечения соединяем.  

На перпендикуляре откладываем длину данного катета, ставим точку А - это вторая вершина треугольника.  

2) От С откладываем отрезок СК, равный сумме второго катета и гипотенузы.  

Соединим К и А 

3) Из А и К как из центров раствором циркуля больше половины АК проведем две полуокружности. Соединим точки их пересечения и продлим, если нужно, до пересечения с СК.  

Обозначим это пересечение В, а пересечение с АК точкой М.  

М - середина АК.  

Соединим А и В.  

Треугольник АВК - равнобедренный: АМ=МК по построению,  МВ - высота и медиана.  

АВ=КВ

В треугольнике АВС   сумма длин сторон АВ и ВС  равна СК. Следовательно, треугольник АВС - искомый.

В нем АС - заданный катет, АВ+ВС =СК, т.е. Заданной сумме двух других сторон.  

(Можно построение провести немного иначе: Провести в ∆ САК  из середины АС параллельно СК прямую до пересечения с АК в точке М, которая разделит АК пополам, а затем провести к М перпендикуляр МВ, отметив по обе стороны от М центры 3 и 4 окружностей и далее как при возведении перпендикуляра СА).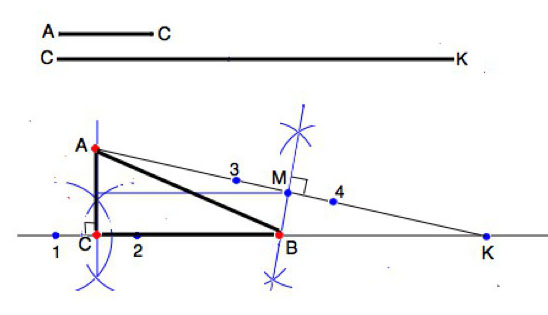

---

1) Строим прямоугольный треугольник АBC, у которого катет AB равен катету данному в условии, а катет AC равен данной по условию сумме двух других сторон
2) Проводим серединный перпендикуляр к гипотенузе BC, который пересекает AC в точке D.
Тогда треугольник ABD искомый, т.к. СBD - равнобедренный (CD=DB, построенный серединный перпендикуляр в нем является высотой и медианой). Значит AD + DB = AD + DC = AC, что и требовалось.