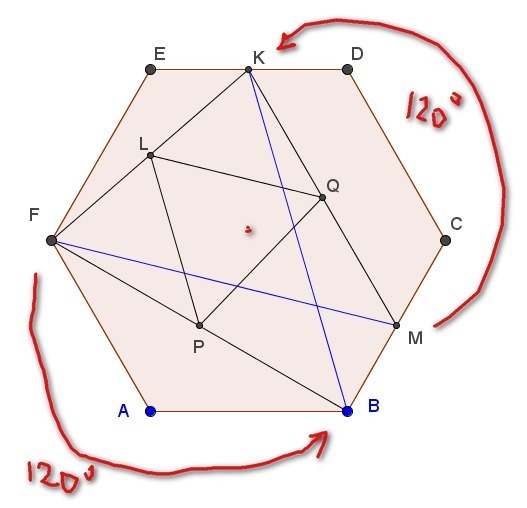
ABCDEF- правильный шестиугольник.
М- середина ВС, К- середина DE, L- середина FK, P- середина BF, Q- середина MK.
Доказать, что треугольник PQL правильный

Решение:

LQ - средняя линия треугольника FKM, значит она равна половине FM и параллельна ей.
LP - средняя линия треугольника FKB, значит она равна половине BК и параллельна ей. Но FM переходит в BК при повороте на 120° вокруг центра 6-угольника, т.е. FM=BK и угол между прямыми FM и BK равен 120° (или 60°). Отсюда LQ=LP и угол между ними тоже 60°, т.е. PQL - правильный.

Пусть стороны 6-угольника равны 1.
Векторы EF=DO=OA=CB=a;
ED=FO=OC=AB=b;
FA=EO=OB=DC=a+b;
LP=LF+FP=KF/2+(FO+FA)/2=(KE+EF)/2+(FO+FA)/2=
(-b/2+a+b+a+b)/2=a+3b/4;
|LP|^2=(a+3b/4)(a+3b/4)=a·a+(9/16)b·b+2(3/4)a·b=
1+9/16+2·1·(3/4)·(-1/2) =13/16
LQ=LK+KQ=FK/2+KM/2=(FE+EK)/2+(KD+DC+CM)/2=
(-a+b/2+b/2+a+b+a/2)/2=a/4+b;
|LQ|^2=(1/16)a·a+b·b+ 2·(1/4)a·b=
1/16+1-1/4=13/16
LP·LQ=(a+3b/4)·(a/4+b)=a·a/4+3b·b/4+a·b+3a·b/16=
1/4+3/4-1/2-3/32=13/32
cos PLQ=(LP·LQ)/(|PL|·|LQ|)=(13/32)/(13/16)=1/2⇒∠PLQ=60°⇒
ΔPLQ - равносторонний