Известно, что в шестиугольнике А1А2А3А4А5А6 все углы равны. Найдите длину отрезка А1А6, если длины отрезков А2А3, А3А4, А5А6 равны 3, 4 и 1 соответственно.

Решение:

Углы данного шестиугольника равны, следовательно, он выпуклый. Сумма углов выпуклого многоугольника вычисляется по формуле N=180°(n-2), где N –сумма углов, n - количество сторон, а, значит, и углов.   

                   N=180°•(6-2)=720°.  

Каждый из равных углов шестиугольника равен 720°:6=120°.

Продлим  А₂А₃ и А₄А₅ до их пересечения в точке К. 

Продлим А₄А₅ и А₁А₆ до их пересечения  в точке М. 

Продлим А₄А₃ и А₁А₂ до их пересечения в точке С.  

 Сумма внутреннего и внешнего угла при каждой из вершин выпуклого многоугольника составляет развернутый угол = 180°.  

Углы, смежные с углами при вершинах шестиугольника, равны 180°-120°=60°.

Тогда в ∆ А₂СА₃, ∆ А₃КА₄ и ∆ А₅МА₆  углы  при их основаниях (сторонах шестиугольника) равны  60°, и  

∆ А₂СА₃, ∆ А₃КА₄ и ∆А₅МА₆ – равносторонние.  

 ∠КА₄А₃=∠КМА₁, они соответственные при пересечении СА₄ и А₁М секущей КМ. Равенство соответственных углов при пересечении двух прямых третьей - признак параллельности ⇒  

                        СА₄║МА₁. 

Аналогично из равенства накрестлежащих углов при А₄ и С  доказывается КМ║СА₁. 

Стороны четырехугольника СА₁МА₄ лежат на параллельных прямых, ⇒ они попарно параллельны. ⇒ СА₄МА₁ - параллелограмм.  

МА₁=СА₄=СА₃+А₃А₄=7

А₁М=СА₄=7

А₁А₆=7-А₆М=7-1=6.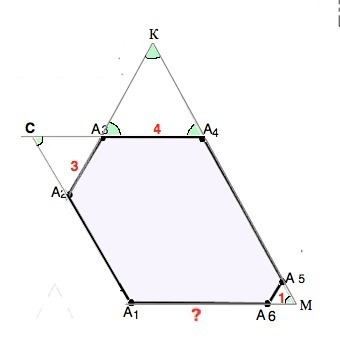