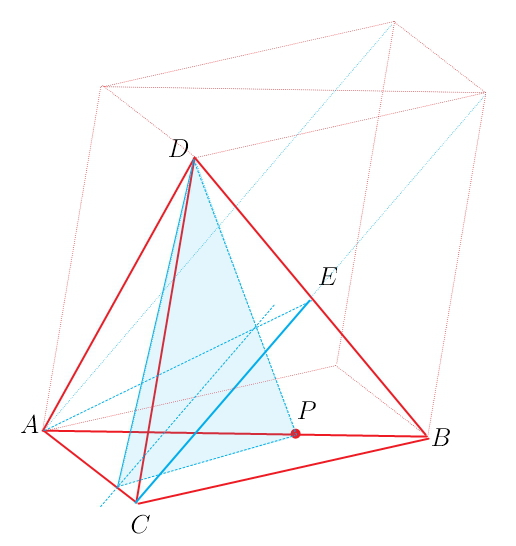
Каждое ребро тетраэдра DABC равно 2 см. Постройте сечение тетраэдра плоскостью, проходящей через точки B.C и середину ребра AD вычислите периметр сечения

Решение:

Так как все ребра тетраэдра равны, то мы имеем правильный тетраэдр (все грани правильные треугольники). На середине ребра АD обозначим точку О. Точка О и В лежат в одной плоскости ADB, следовательно, плоскость сечения пересечет плоскость ADB по прямой ОВ. Аналогично проводим прямую через т. С и О. СОВ-искомое сечение.

Сторона CD=2cм (нам уже известно), так как О-середина АВ, то АО=OD=1см. ОС и ОВ вяляются медианами и высотами треуг. АСD и ABD соответственно. По теореме Пифагора ОС=ОВ=√(4-1)=√3см

Р=ОС+ОВ+СВ=2+√3+√3=2+2√3см

DABC – тетраэдр, углы DBA=DBC=90, DB = 6, AB = BC = 8, AC = 12. Постройте сечение тетраэдра плоскостью, проходящей через середину ребра DB и параллельной плоскости ADC. Найдите площадь сечения.

В этом тетраэдре грани ABD=CBD по двум катетам (АВ=СВ по условию, DB-общий, а угол В у них прямой).

Строим сечение. Точка Е-середина ребра DB. Сечение проходит параллельно плоскости ADC. Стороны AD и CD принадлежат этой плоскости, значит сечение будет параллельно этим сторонам. Возьмем грань CBD. Прямая, по которой будет проходить сечение, параллельна CD и проходит через середину DB (точку Е), будет средней линией для треуг. CBD. Значит на середине канта СВ отмечаем точку К и проводим прямую ЕК. Аналогично для грани ABD. Точка М - середина канта АВ. МЕК - искомое сечение. МЕК - равнобедренный треуг. МЕ=ЕК. МК - средняя линия для треуг. АВС. МК=АС/2=12/2=6

ЕК=√(КВ^2+EB^2), КВ=ВС/2=8/2=4,  ЕВ=DB/2=6/2=3.

ЕК=√(16+9)=5,  МЕ=ЕК=5, МК=6.

В треуг. МЕК проведем высоту ЕО (она же и медиана).

МО=ОК=МК/2=6/2=3

ЕО=√(25-9)=4

S(сечения МЕК)=ЕО*ОК=4*3=12

Ответ: 12

---

Так как ∠DBA=∠СВD=90°, треугольники АВD и СВD прямоугольные и по соотношению катетов - "египетские". ⇒ ребра АD и СD равны 10 (можно проверить по т. Пифагора)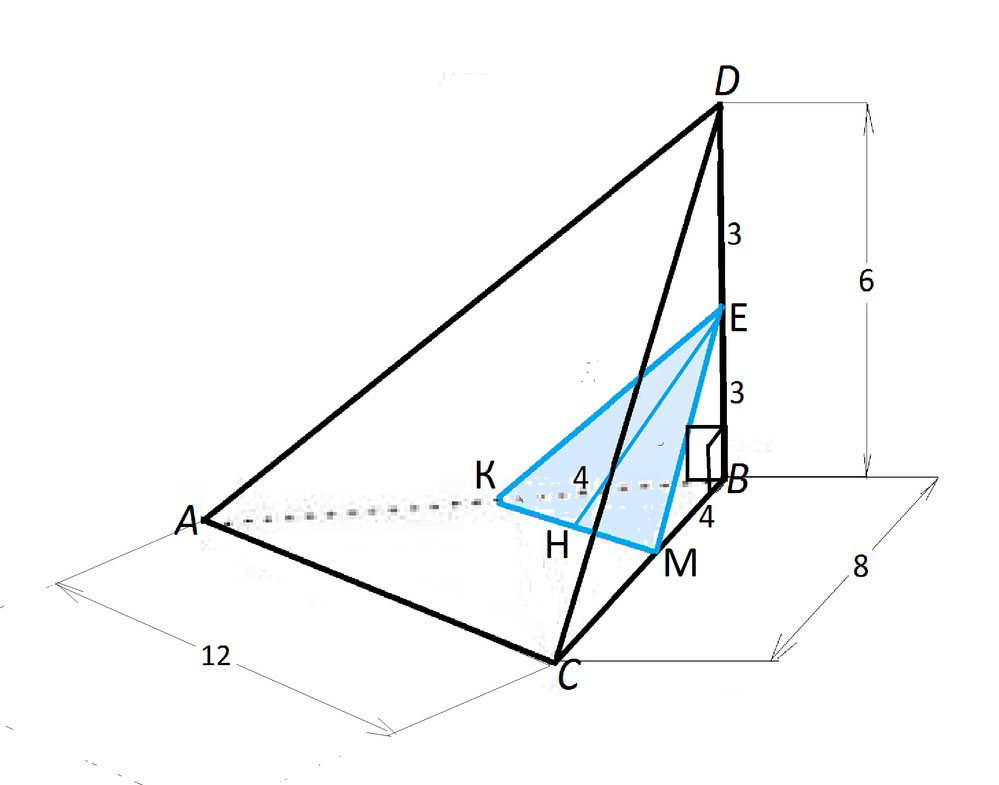
Сечение проходит через середины DB, ВА и ВС
Обозначим эти середины Е, К, М соответственно.
Получим КМ║АС и как средняя линия треугольника АВС равна АС:2=6 
КЕ║АD и ЕМ║СD. Они средние линии боковых граней и их длина равна половине АД=ДС и равна 5
Сечение - равнобедренный треугольник с боковыми сторонами, равными 5 
 и основанием 6
 Высота ЕН этого треугольника делит ∆ КЕМ на два "египетских" и равна 4.
(тот же результат получим по т. Пифагора)
S∆ КЕМ=KM*ЕН:2=12(единиц площади)

Постройте сечение тетраэдра плоскостью, проходящей через точки С и М паралельно прямой а.

1) проводим прямую l параллельную прямой а и проходящую через точку С.

2)  l пересекается с прямой АВ в точке К.

3) Точки К и М лежат в плоскости грани DAB, поэтому можем их соединить. КМ пересекается с BD в точке Р.

4) MPC -  искомое сечение, т.к. прямая СК принадлежит плоскости сечения и СК параллельна прямой а. По признаку параллельности прямой и плоскости прмая а параллельна плоскости MPC.

Основанием тетраэдра ABCD является прямоугольный треугольник ABCD, в котором AB = BC = 4. Боковые ребра = 6. Построить сечение тетраэдра плоскостью, проходящей через середину АС перпендикулярно этому ребру. Найти площадь сечения.

Сечение строится так - через середину АС и ребро DB проводится плоскость. Это будет прямоугольный треугольник с катетом 2*корень(2) и гипотенузой 6. Второй катет равен 2*корень(7), а площадь 2*корень(14).

Необходимые пояснения:

В основании лежит прямоугольный равнобедренный треугольник, середина АС это центр описанной окружности. Поэтому вершина пирамиды D проектируется именно туда, поскольку она равноудалена от вершин (значит и проекция её равноудалена от вершин). Поэтому плоскость АСD перпендикулярна плоскости АВС. Если М - середина АС, то DM  и ВМ - медианы в равнобедренных теругольниках, то есть они перпендикулярны АС, то есть угол между ними - это двугранный угол между перпендикулярными плоскостями )). ВМ = 4 * корень(2)/2 = 2 * корень(2). А боковое ребро задано. Отсюда находим DM.

В тетраэдре DABC точка M-середина AC, DB = 6, MD = 10, угол DBM = 90 градусов. Постройте сечение тетраэдра плоскостью, проходящей через середину ребра DC параллельно плоскоскости DMB и найдите площадь сечения

Обозначим середину отрезка DC точкой любой к примеру Z. Проведем линию из точки Z к середине отрезка MC. Обозначим ее также, к примеру, U. От этих двух точек проведем линии к середине отрезка BC. Обозначим, к примеру, эту точку, как L. У нас получился треугольник ZUL, подобный треугольнику DMB. А так как эти линии которые мы проводили, были проведены из середины BC, DC и MC, то они будут относиться к линиям треугольника DMB, как 1:2, то есть в два раза меньше. Слеовательно ZU=5, ZL=3. Угол ZUL = 90. ZU гипотенуза треугольника ZUL, ZL один из его катетов, следовательно UL = 4 (египетский треугольник). S=½(ah)=½(4*3)=6 см².

В тетраэдре DABC DA=DC=13, AC=10, E-середина BC. Постройте сечение тетраэдра плоскостью, проходящей через точку E параллельно плоскости ADC, и найдите площадь сечения.

Построение сечения: 

Сделаем рисунок тетраэдра.  

На середине ВС отметим точку Е.  

Проведем ЕК параллельно АС.

На боковых гранях ВСD и ВАD проведем  из  Е и К параллельно ребрам СD и АD прямые до пересечения на ребре в точке М.  

КМ и ЕМ - средние линии ∆ ADB  и ∆  CDB

В плоскости КМЕ пересекающиеся прямые КЕ и ЕМ соответственно  параллельны пересекающимся прямым АС и DС.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны ⇒

плоскость сечения КМЕ || плоскости ADC. 

––––––––––––––––

В тетраэдре боковая грань  ADC – равнобедренный треугольник по условию. Треугольники КМЕ и АDC подобны, т.к. стороны ∆ МКЕ - средние линии ∆ АВС,  ⇒ k=АС: КЕ=2

Высота DН равнобедренного треугольника АDС - его медиана.  ⇒ АН=НС=5,  ∆ ADH=CDH - прямоугольные.  

По т. Пифагора DН=12, но можно обойтись без вычислений, если вспомнить, что стороны треугольника АDН из часто встречающихся в задачах Пифагоровых троек с отношением 13:5:12

Тогда S ∆ ADC = DH • AH = 12 • 5 = 60

Отношение площадей подобных фигур равно квадрату коэффициента подобия.

S ∆ ADC:S ∆ KME=k²= 4

S ∆ KME=60:4=15 (ед. Площади)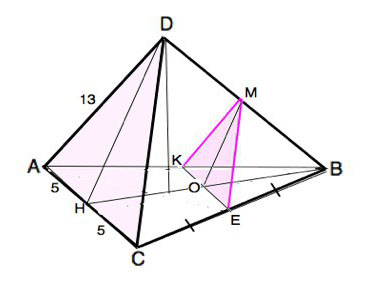

Постройте сечение тетраэдра плоскостью, проходящей через точки С и К и параллельной а.

1) проводим прямую l, параллельную прямой а и проходящую через точку С. 2)  l пересекается с прямой АВ в точке К. 3) Точки К и М лежат в плоскости грани DAB, поэтому можем их соединить. КМ пересекается с BD в точке Р. 4) MPC -  искомое сечение, т.к. прямая СК принадлежит плоскости сечения и СК параллельна прямой а. По признаку параллельности прямой и плоскости прмая апараллельна плоскости MPC.

Как построить сечение тетраэдра плоскостью, проходящей через данные точки М, N, К и в задачах 1-3 найти периметр сечения, если М, N, К – середины ребер и каждое ребро тетраэдра равно а?

Измеряете линейкой длину ребра на рисунке, делите её пополам и ставите точку. И так на трех ребрах идущих в одну вершину. После соединения двух точек на одной гране получите прямую, параллельную ребру. Например, на грани АДВ прямая КМ параллельна ребру АВ.  Поскольку К и М середины ребер, то линия КМ является средней линией треугольника АДВ. А средняя линия треугольника равна половине той стороны треугольника, которой она параллельна. Т.е. КМ = АВ/2 = а/2. Соединяя линиями все точки, получите прямые на гранях. Поскольку каждое ребро тетраэдра равно  а, то все отрезки, соединяющие середины ребер будут равны а/2, т.к. Все эти отрезки будут являться средними линиями треугольных граней. Таким образом, периметры сечений равны 1) 3а/2; 2) 3а/2; 3) 4а/2 = 2а

Длина ребра тетраэдра ABCD равна 4 см. Постройте сечение тетраэдра плоскостью, проходящей через O - середину BC и перпендикулярной CD. Вычислите периметр сечения

Сечение построить легко. Опустили из т. О перпендикуляр на CD в точку Н, потом из т. Н под углом 90 градусов провели отрезок НК до пересечения С ребром АС в т. К, и наконец соединили Н и О, получили в сечении треугольник ОНК. Дальше на рисунке

В тетраэдре DABC точка М — середина AD, Р принадлежит DC и DP:PC =1:2. Постройте сечение тетраэдра плоскостью, проходящей через точки М и Р и параллельной ВС.
Найдите площадь сечения, если все ребра тетраэдра равны 6.

В сечении имеем равнобедренный треугольник МРК. МК = МР.
Сторона РК (по свойству подобных треугольников) равна 1/3 части ВС: РК = 6/3 = 2.
Так как углы всех граней тетраэдра равны 60°, то длину сторон МК и МР находим по теореме косинусов из треугольника МДК:
(по условию МД = 3, а КД = РД = 6/3 = 2)
\( MK= \sqrt{3^2+2^2-2\cdot 3\cdot 2\cdot cos60}= \sqrt{9+4-6} = \sqrt{7} =2.64575. \)
Теперь все стороны известны и по Герону находим площадь:
       a          b          c                  p               2p                S
2.64575     2    2.64575    3.64575  7.2915026   2.4494897 
cos A = 0.3779645    cos B = 0.7142857    cos С = 0.377964473
Аrad = 1.1831996    Brad = 0.7751934      Сrad = 1.18319964
Аgr = 67.792346      Bgr = 44.415309         Сgr = 67.7923457

В тетраэдре DABC P принадлежит AB, CE - медиана грани DCB. Построить сечение тетраэдра плоскостью, проходящей через точки D и P параллельно CE

Сечение, проходящее через DP -это треугольник, в котором одна сторона уже задана, осталось найти третью вершину.
Эта точка должна лежать на прямой, параллельной СЕ (сечение должно содержать прямую, параллельную СЕ)
(Можно, наверное и не достраивать до параллелепипеда, но так понятнее и лучше видно) У параллелепипеда есть параллельные грани.
DP пересекает плоскость АСЕ в точке пересечения прямых DP и AE
в плоскости АСЕ (это диагональное сечение параллелепипеда) строим параллельную СЕ прямую.
Или просто: DP пересекаем с АЕ и через точку пересечения проводим параллельно СЕ прямую