Дан параллелепипед ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через середину ребра AB параллельно плоскости DBB1.

Решение:

Сначала проводим в паралелепипеде диагонали оснований BD и B1D1. ВВ1D1D и есть та плоскость, параллельно которой нужно построить сечение.

Точка М - середина АВ. Сечение пересекает нижнее основание по прямой МК, где К-середина AD. Боковую грань АА1В1В пересекает по прямой ММ1, где М1-середина А1В1. Боковую грань AA1D1D пересекает по прямой КК1, где К1-середина A1D1. ММ1К1К - искомое сечение.

В параллелепипеде АВСДА’В’С’Д’ точка P принадлежит АД, К принадлежит ВС. Постройте сечение параллелепипеда плоскостью, проходящей через точки Р и К и параллельной АА

На грани ВСC’B’ проводится прямая КК’ II ВВ’ (до пересечения с В’C’, К’ лежит на В’C’)

Точно также на грани ADD’A’ проводится прямая РР’. Точки Р’ и К’ надо соединить. Получается параллелограмм РКК’P’.

Обоснование этого простого построения тоже очень просто. Плоскость сечения параллельна АА’, поэтому любая прямая в этой плоскости тоже параллельна АА’, а, следовательно, и тем прямым, которые заведомо параллельны AA’, в частности, ребрам DD’, CC’,  BB’. Таким образом, линия пересечения плоскости сечения с плоскостью ВСС’В’ параллельна ВВ’. И также и с плоскостью ADD’A’.

Дан параллелепипед АВСDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через точки М, N и К, являющиеся серединами рёбер АВ, ВС и DD1

Точки М и N принадлежат грани АВСD параллелепипеда и плоскости сечения.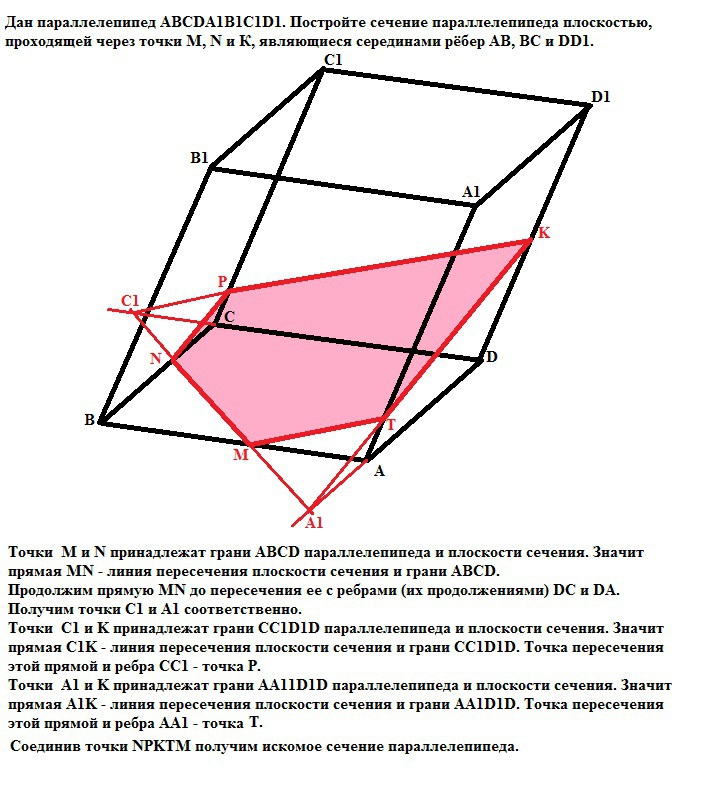
Значит прямая MN является линией пересечения грани АВСD параллелепипеда и плоскости сечения.
Продолжим прямую MN до пересечения ее с ребрами DС и DA. Получим точки С1 и А1 соответственно.
Точки С1 и К принадлежат грани СС1D1D параллелепипеда и плоскости сечения. Значит прямая С1К является линией пересечения грани СС1D1D параллелепипеда и плоскости сечения. Точка пересечения этой прямой и ребра СС1 - точка Р.
Точки А1 и К принадлежат грани АА1D1D параллелепипеда и плоскости сечения. Значит прямая А1К является линией пересечения грани АА1D1D параллелепипеда и плоскости сечения. Точка пересечения этой прямой и ребра АА1 - точка Т.
Соединив точки NPKTM получим искомое сечение параллелепипеда.

Точка М лежит на ребре ВС параллелепипеда ABCDA1B1C1D1. Постройте сечение параллелепипеда плоскостью, проходящей через точку М и параллельной плоскости B1C1D

Сечением в данном случае будет сечение, касательное к параллелепипеду в отрезке BC
Коричневый цвет (сечение "B1C1D")
Голубой цвет (сечение параллельное плоскости "B1C1D" и проходящее через точку М)

На ребрах АА1 и СС1 параллелепипеда ABCDA1B1C1D1 расположены соответственно точки М и N так, что АМ: АА1=m, CN:CC1=n. Построить сечение параллелепипеда плоскостью, проходящей через точки M и N параллельно диагонали BD основания. Определить в каком отношении эта плоскость делит ребро ВВ1.

На рисунке параллелепипед прямой, но это не обязательно по условию, просто так привычнее.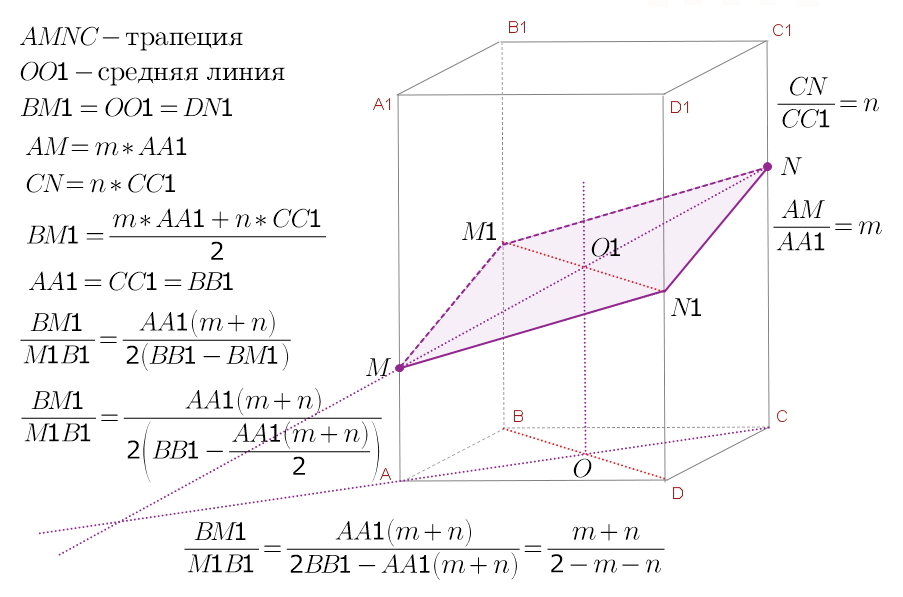
Нигде перпендикулярность плоскостей в рассуждениях не использовалась.
AMNC в любом случае -это трапеция.
Средняя линия трапеции равна полусумме длин оснований.
Если искомое отношение записать чуть иначе, получится немного другое выражение:
B1M1 / M1B = (BB1 - M1B) / M1B = (BB1 / M1B) - 1 = (2 / (m+n)) - 1
это просто обратная величина.

Основание прямоугольного параллелепипеда ABCDA1B1C1D1 - квадрат. Точка K - середина ребра B1C1. Постройте сечение параллелепипеда плоскостью, которая проходит через прямую AK и параллельна прямой CC1. Вычислите площадь боковой поверхности параллелепипеда, если периметр сечения равен \(5\sqrt{5+4}\) см и AB=5 см

Периметр сечения - прямоугольник, в котором \( AA_1=KO,\ AO=A_1K \)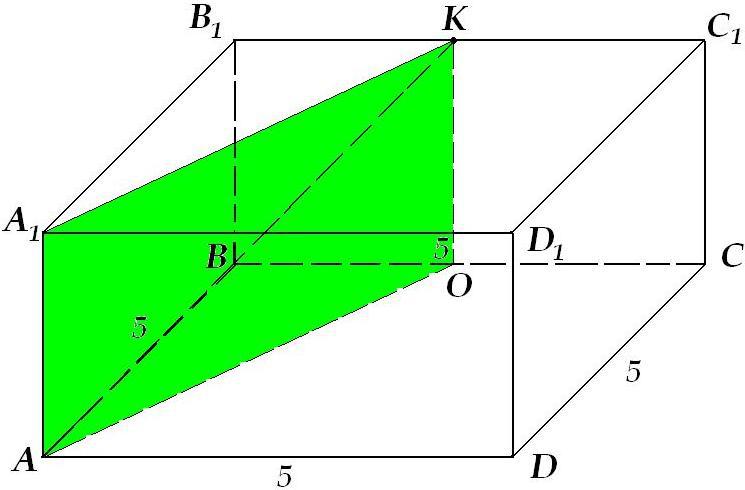
\( AO= \sqrt{AB^2+BO^2}=\sqrt{5^2+( \frac{5}{2})^2}= \sqrt{5^2+ \frac{5^2}{4}}=\\=\sqrt{ \frac{4\cdot5^2+5^2}{4}}= \sqrt{ \frac{5\cdot5^2}{4}}= \frac{5 \sqrt{5}}{2}\ cm \)
\( AA_1= \frac{P-2AO}{2}= \frac{5 \sqrt{5}+4-2\frac{5 \sqrt{5}}{2}}{2}=\frac{5 \sqrt{5}+4-5 \sqrt{5}}{2}= \frac{4}{2}=2\ cm \)
Периметр основания равен:
\( P_{oc.}=4\cdot{AB}=4\cdot5=20 \) см
Площадь боковой поверхности равна:
\( S=P_{oc.}\cdot AA_1=20\cdot2=40 \) см²

В параллелепипеде ABCDA1B1C1D1 все грани - квадраты, со стороной, равной 8 см(куб). Точки P M T соответвсуют серединам рёбер A1B1, C1C, AD. Постройте сечение параллелепипеда плоскостью, проходящей через точки P M T и найдите площадь сечения

Через параллельные прямые А1В1 и DC проведем плоскость (она определена и единственна). Эта плоскость включает в себя прямые А1D и В1D, т.к. Концы этих прямых лежат в этой плоскости. Иначе говоря, плоскости DA1B1 и А1В1DC совпадают.
Через середину AD - точку К в плоскости ADD1A1 проведем прямую КМ параллельно DA1. Причем, точка М поделит АА1пополам (параллельные прямые делят стороны угла в одинаковом отношении). Также в плоскости ABCD через точку К проведем прямую КТ параллельно АВ. В плоскости АВВ1А1 через точку М проведем прямую МР параллельно АВ. Она пересечет ВВ1 в середине. Соединим точки Т и Р. ТР параллельна СВ1, т.к. Является средней линией в треугольнике ВСВ1. 
Плоскость КМРТ параллельна плоскости А1В1DC по признаку параллельности плоскостей (МК||А1D и КТ||DC по построению).
Прямоугольные треугольники А1DА и МКА подобны по острому углу (∠А1DА=∠МКА как соответственные при параллельных прямых А1D и МК и секущей AD). Поэтому А1D: МК=AD: АК=2
А1D/2=МК. В треугольнике ВВ1С РТ=В1С/2 как средняя линия. МР=АВ, КТ=АВ соответственно из прямоугольников АВМР и АВКТ.