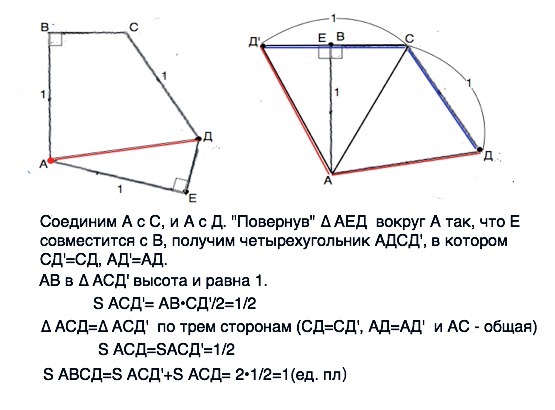
В выпуклом пятиугольнике ABCDE углы ABC и CDE равны по 90°, а каждая из сторон BC, CD и AE равна 1 и сумма сторон AB и DE равна 1. Найдите площадь пятиугольника

Решение:

Продлим АВ за точку А, пусть F лежит на этом продолжении и FB = 1.

FBCD - квадрат со стороной 1. Точка пересечения АЕ и FD обозначим за К.  

В условии ED + AB = 1, это означает, что FA = ED;

Если провести окружность радиусом 1 и центром в А, то она коснется DC в точке Р, причем АР перпендикулярно DC, FA = PD. Окружность пройдет через точку Е (АЕ =1),

и DE = DP. Поэтому  DE - касательная, и треугольник EDK прямоугольный, угол АЕD прямой. Значит треугольники FAK и KED равны, равны и их площади. Поэтому площадь пятиугольника равна площади квадрата, то есть 1.

В выпуклом пятиугольнике ABCDEравны четыре стороны: AB=BC=DE=AE=2 углы при вершинах A и B прямые а при вершине E равен 120. Найдите площадь пятиугольника

Разбиваем многоугольник на треугольники, проводим линии АС и АД, треугольник АВС прямоугольный уголВ=90, равнобедренный, АВ=ВС=2, уголВАС=уголАСВ=90/2=45, площадь АВС=1/2*АВ*ВС=1/2*2*2=2, АС=корень(АВ в квадрате+ВС в квадрате)=корень(4+4)=2*корень2, треугольник АДЕ равнобедренный, АЕ=ДЕ=2, уголЕ=120, уголДАЕ=уголАДЕ=(180-120)/2=30, площадь АДЕ=1/2*АЕ*ДЕ*sin120=1/2*2*2*корень3/2=корень3, АД в квадрате=АЕ в квадрате+ДЕ в квадрате-2*АЕ*ДЕ*cos120=4+4-2*2*2*(-1/2)=12, АД=2*корень3, уголСАД=уголА-уголВАС-уголДАЕ=90-45-30=15, площадь САД=1/2*АС*АД*sin15=1/2*2*корень2*2*корень3*sin15, sin15=sin(45-30)=sin45*cos30-cos45*sin30=(корень2/2*корень3/2) - (корень2/2*1/2)=корень2/4 *(корень3 -1), площадь САД=1/2*2*корень2*2*корень3 *(корень2/4 *(корень3 -1))=корень3*(корень3-1)=3-корень3, площадь АВСДЕ=площадь АВС+площадьАДЕ+площадьСАД=2+корень3+3-корень3=5

Пусть ABCDE — выпуклый пятиугольник такой, что AB= AE =CD =1, ∠ABC =∠DEA=90◦
и BC + DE = 1. Вычислите площадь пятиугольника ABCDE.

Соединим А с С, и А с Д. "Повернув" ∆ АЕД  вокруг А так, что Е совместится с В, получим четырехугольник АДСД’, в котором СД’=СД, АД’=АД.

АВ в ∆ АСД’ высота и равна 1. СД’=ВС+ДЕ=1 

 S АСД’= АВ•СД’=1•1:2=1/2

 ∆ АСД=∆ АСД’  по трем сторонам (СД=СД’, АД=АД’  и АС - общая)

S АСД=SАСД’=1/2

S АВСД=S АСД’+S АСД= 2•1/2=1(ед. площади)