На растоянии 4см от центра шара проведено сечение. Хорда, удаленная от


Главная Научный калькулятор
Меню Алгебра Геометрия Основные понятия Аксиомы планиметрии Углы Перпендикулярные и параллельные прямые Перпендикуляр и наклонная Круг (окружность) Треугольник Четырехугольник Параллелограмм Трапеция Многоугольники Основные понятия стереометрии Аксиомы стереометрии Прямые в пространстве Пересекающиеся прямые Параллельные прямые Скрещивающиеся прямые Прямая и плоскость в пространстве Перпендикулярность прямой и плоскости Параллельность прямой и плоскости Угол между прямой и плоскостью Теорема о трех перпендикулярах Формула двойного проектирования Плоскости в пространстве Пересекающиеся плоскости Параллельность плоскостей Перпендикулярность плоскостей Площадь проекции плоской фигуры на плоскость Многогранники: Пирамида Призма Тела вращения: Цилиндр Конус Шар (Сфера) Объем тел вращения Задачи по геометрии Примеры решений Вспомогательные материалы: Таблицы Брадиса Исследование функций Асимптоты. Первая производная. Вторая производная. Графики функций Задачи по функциям Тригонометрия Тригонометрические неравенства	Треугольник : Равнобедренный треугольник : Прямоугольный треугольник : Четырехугольник : Параллелограмм : Ромб : Прямоугольник : Трапеция : Многоугольники : Круг и окружность : Прямые и плоскости : Пирамида : Системы координат : Цилиндр : Конус : Углы : Призма : Параллелепипед : Сфера и Шар : Построения На растоянии 4см от центра шара проведено сечение. Хорда, удаленная от центра этого сечения на корень5 см стягивает угол 120’. Найдите объем шара и площадь его поверхности. Решение: Изобразим круг, который является сечением шара. В нем покажем центр сечения О1, хорду АВ, отрезок О1Д, являющийся расстоянием от О1 до хорды АВ, Хорда стягивает угол в 120⁰, значит, центральный угол АО1В равен 120⁰. О1Д делит хорду пополам. Рассмотрим прямоугольный ΔАДО1. В нём угол АДО1 = 90⁰, угол ДО1А = 120⁰:2 = 60⁰, т. К высота равнобедренного ΔАО1В является и биссектрисой. ОА = r - радиус рассматриваемого кругового сечения является гипотенузой в ΔАДО1. АО1 = ДО1: cos 60⁰ = √5: 0,5 = 2√5(см). Осталось найти радиус шара. Изобразим шар с центром в точке О, расстояние ОО1 до сечения задано (ОО1 = 4 см) проведём след сечения - прямую АО1В параллельную диаметру шара. Рассмотрим прямоугольный ΔАОО1, в котором биссектрисой является радиус шара R=АО, катетами ОО1 = 4см и АО1 = 2√5см. Используем иеорему Пифагора: R = √(4² +(2√5)²) = √(16 +20) = √36 = 6(см) Объём шара вычисляется по формуле V = 4π·R³/3 = 4π·6³/3 = 288π(см³) Площадь поверхности шара вычислим S = 4π·R² = 4π·6² = 144π(см²) Начнем с плоскости сечения шара. Смотрим на нее как бы сверху - видим круг. Соединим концы хорды, стягивающей угол 120градусов, и ее середину с центром окружности, ограничивающей плоскость сечения. Получим прямоугольный треугольник с острым углом 30 градусов, против которого лежит катет, равный √5 Радиус r, как гипотенуза этого треугольника, равен 2√5 Теперь представим себе сечение, которое проходит перпендикулярно плоскости данного сечения. Диаметр сечения, которое нам было дано, является теперь хордой, расстояние от центра которой до центра шара равно 4 см. Рассмотрим треугольник, который получится, когда мы соединим центр шара и конец этой хорды. 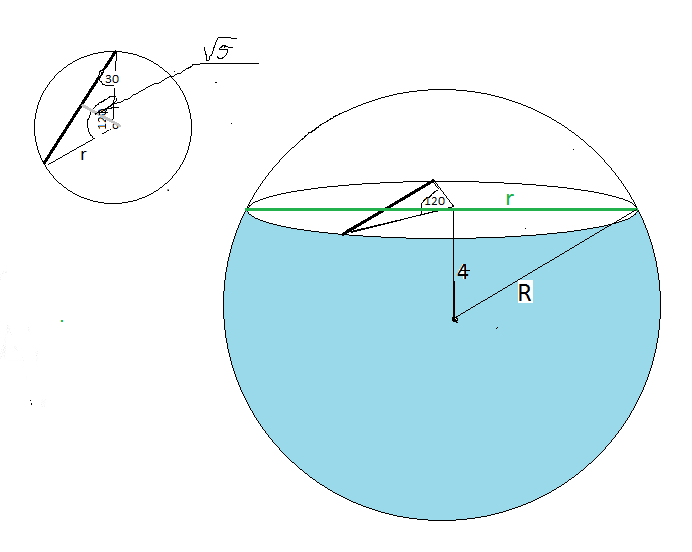Радиус R шара здесь - гипотенуза прямоугольного треугольника, катеты которого нам известны. R²= (2√5)²+4²=20+16=36 R=√36=6 cм Площадь поверхности сферы равна учетверенной площади большого круга: S=4 π R² S=4 π 36=144 см² Объем шара* в полтора раза меньше, чем объем описанного вокруг него цилиндра. V=4/3 π R³ V=4π216:3=288π см³ Найдите объем шара, если площадь его сечения равна 144π. Расстояние от центра шара до полскости сечения равно 5 см. Так как сечение шара есть окружность, зная ее площадь найдем радиус: \( S=\pi R^2 \) \( R_1=\sqrt{\frac{S}{\pi}} \) \( R_1=\sqrt{\frac{144\pi}{\pi}}=12 \) Тогда исходя из прямоугольного треугольника* во вложении находим радуис сферы:* \( R=\sqrt{h^2+R_1^2}=\sqrt{5^2+12^2}=13 \) Тогда объем сферы равен: \( V=\frac{4}{3}\pi R^3=\frac{4}{3}13^3\pi=\frac{8788}{3}\pi \) 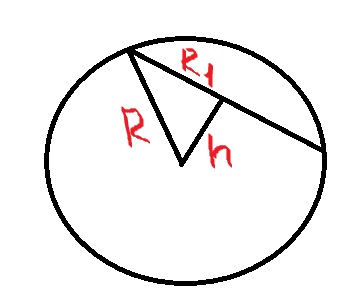В шар вписан тетраэдр с ребром равным 12 см. Определите объём шара Тетраэдр ДАВС, Д-вершина, в основании треугольник АВС, точки А, В, С, Д лежат на поверхности шара, АС=АВ=СВ=АД=СД=ВД=12. О-центр шара, О1-центр треугольника АВС, ДМ-диаметр шара проходит через точки О и О1, АН-высота треугольника=сторонакорень3/2 =12корень3/2=6корень3, АО1=2/3АН=6корень32/3=4корень3, треугольник АДО1 прямоугольный, ДО1=корень(АД в квадрате-АО1 в квадрате)=корень(144-48)=4корень6, треугольник ДАМ прямоугольный, уголДАМ=90, опирается на диаметр, АД в квадрате=ДМДО1, 144=ДМ4корень6, ДМ=144/(4корень6)=6корень6, радиус шара=ДМ/2=6корень6/2=3корень6, объем шара=4/3 пирадиус в кубе=4/3пи(3корень6) в кубе=216пикорень6 В шар вписан тетраэдр с ребром равным 1 см. Определите объём шара. Радиус окружности, в которую вписано основание тетраэдра находим из прямоугольного треугольника, где гипотенуза - искомый радиус, а катет - половина ребра. Угол между ними 30°. r = (1/2) / cos 30° = (12) / (2√3) = 1 / √3. Высоту тетраэдра находим по Пифагору: H = √(1² - (1/√3)²) = √(2/3). Теперь рассмотрим осевое сечение шара, проходящее через ребро тетраэдра. Высота в прямоугольном треугольнике (она же радиус r), проведенная из вершины прямого угла, делит его на два подобных. Из подобия запишем пропорцию: H/1 = 1/D. Отсюда D = 1/H = 1 / (√(2/3)) = √(3/2). Объём шара равен V = (1/6)πD³ = (1/6)π(3/2)(√(3/2) = 0,96191. Через точку, расположенную на сфере, проведены два взаимно перпендикулярных сечения, площади которых равны 11π см и 14π см. Найдите объём шара и площадь сферы. Так как сечения перпендикулярны, значит их радиусы перпендикулярны. В то же время перпендикулярны отрезок опущенный из центра шара в центр каждого сечения. Там образуется прямоугольник, большая диагональ которого - это радиус шара из его центра к точке на сфере, одна сторона -это Rпервого сечения, другая - R второго сечения. Площадь круга равна S=πr² площади сечений известны, можем найти их радиусы R1=√11 R2=√14 Теперь найдем радиус шара из указанного выше прямоугольника Rш=√(R1²+R2²)=√(11+14)=5 V=4πR³ш/3=4π125/3=прибл 523 S=4πR²ш=4π25=приблизительно 314 Найдите объем шара если площадь сечения проведенного на расстоянии 4 см от центра шара равна 9 пи см/кв. Пусть О - центр шара, А - центр окружности данного сечения, В - точка на шаре такая, что АВ - радиус кругового сечения, ОВ - радиус шара. Тогда ОА - расстояние между центром шара и центром кругового сечения и по условию равно 4. Площадь кругового сечения: \( S=\pi r^2 = 9\pi, r^2=9, r=3=AB \) По теореме Пифагора в ΔОАВ: \( OB=R= \sqrt{16+9}=5 \). Объём шара \( V= \frac{4}{3}\pi R^3= \frac{4}{3}\pi 125= \frac{500\pi}{3} \)