| Главная Научный калькулятор | |
|
|
Докажите, что в выпуклом пятиугольнике сумма длин диагоналей больше периметра и меньше удвоенного периметра.Решение: Диагонали пятиугольника пересекаясь образуют пятиконечную звезду, которая выходит из кусочков x1,x2,x3.x10 и заштрихованного пятиугольника(смотрите рисунок) пусть его периметр равен Po. Откуда верно что: d1+d2+d3+d4+d5=x1+x2+x3.+x10+Po Откуда следует очевидное неравенство : x1+x2+x3.+x10a1 x2+x3>a2 x4+x5>a3 x6+x7>a4 x8+x9>a5 Сложим их попарно: x1+x2+x3.+x10>a1+a2+a3+a4+a5=P Но поскольку x1+x2+x3.+x10P Второе второе уже разобрано в комментарии. 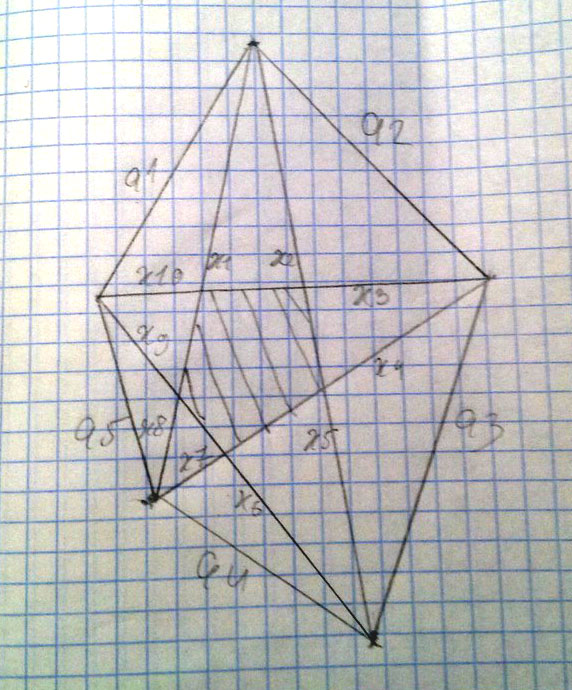 Похожие вопросы:
|