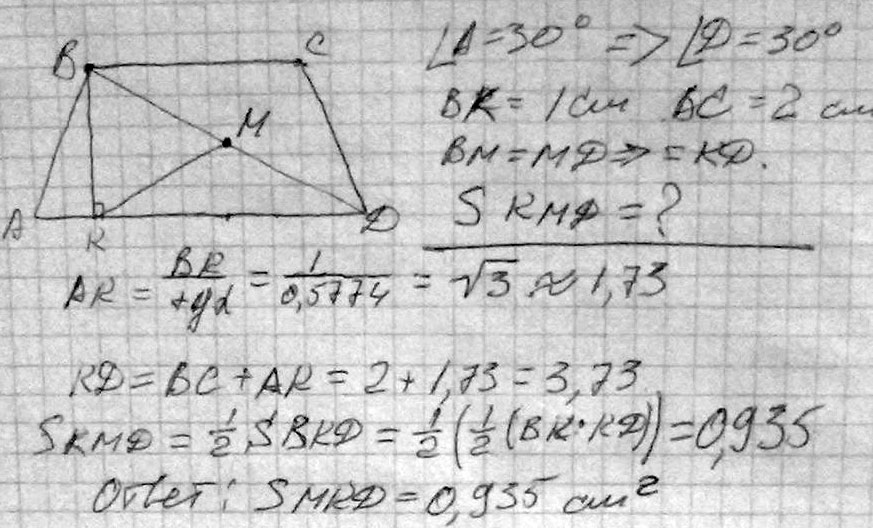
В равнобедренной трапеции ABCD AD II ВС, A = 30°, высота ВК = 1 см, ВС= 2 см. Найдите площадь треугольника KMD, если М - середина отрезка BD.

Решение:
АВСД- трапеция,   МТ перпендикуляр к АД. S=½KD·MT, МТ- средняя линия ΔДВК, МТ=½ВК =½·1=½, КД=КО+ОД  ( СО -перпендикуляр к АД) .ΔАВК=ΔСОД,  ОД=АК;ΔАВК, <К=90⁰,ВК=½АВ(как катет,что лежит против угла в 30⁰), откуда  АВ=2·ВК=2·1=2 , по т. Пифагора АК= =√(АВ²-ВК²)=√(4-1)=√3. КД=2+√3.  S=½ (2+√3)·½=(2+√3)/4
Ответ: (2+√3)/4см²