| Главная Научный калькулятор | |
|
|
Из середины d равносторонего стороны вс треугольника авс проведён перпендикуляр dm к прямой ас. Найти am если АВ =12 смРешение: Δ АВС равносторонний, значит АВ=ВС=АС=12см <А=<В=<С = 60° Построим высоту ВК, которая будет являться и медианой и биссектрисой ΔАВС ⇒АК=КС = ½АС = 6см ∢ΔВКС - прямоугольный DM является средней линией ΔВКС, т,к. ВК параллельно DM, т.D середина отрезка ВС ⇒ и т.М середина стороны КС КМ=МС=½КС = ½*6=3см АМ=АС - МС = 12-3 = 9 см Ответ АМ = 9 см
Проведем высоту BH к стороне AC. Треугольник BHC подобен треугольнику DMC (По 2м сторонам и углу между ними). DC=0.5*BC=6см В равностороннем треугольнике высота является медианой => H - серидина AC и HC=0.5*AC=6см. HC/MC=BC/DC -> DMC=3см AM=AC-MC=9см. 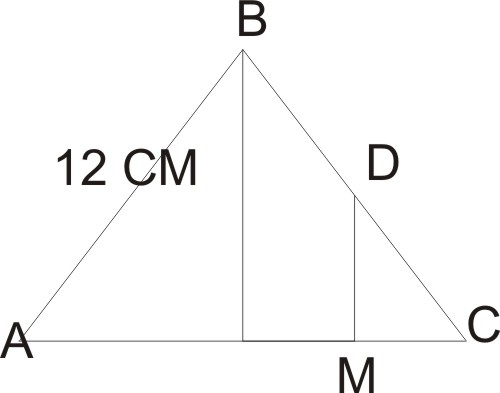 Похожие вопросы:
|