| Главная Научный калькулятор | |
|
|
Дан шестиугольник A1;A2,A3;A4,A5;A6, его стороны A1;A2 и A4;A5,A2;A3 и A5;A6,A3;A4 и A6;A1 попарно равны и паралельны, используя центральную симетрию докажите, что диагонали A1;A4,A2;A5 и A3;A6 данного шестиугольника пересекаются в одной точке.Решение: Все полученные треугольники равны (по стороне и двум углам при ней). Это означает, что диагонали в точке их пересечения делятся пополам. Поэтому у фигуры есть центр симметрии. И все диагонали, соединяющие центрально симметричные вершины проходят через центр симметрии и делятся им пополам. 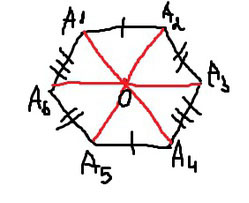 Похожие вопросы:
|