| Главная Научный калькулятор | |
|
|
Найдите сторону правильного десятиугольника, вписанного в окружность с радиусом 5м.Решение: Рассмотрим треугольник, образованный двумя радиусами описанной около декагона (правильного десятиугольника) окружности и его стороной. Это равнобедр. треуг. с боковыми сторонами, равными 5. Угол между радиусами определяется так - 360°/10 = 36°. Сторону декагона можно найти по теореме косинусов: $$ a = \sqrt{R^2+R^2 - 2*R*R*cos36} \\ = \sqrt{50-2*25*0.81} \ = \sqrt{9.5} \\ = 3.082 = 3.1 $$ Ответ: a₁₀ = 3.1м 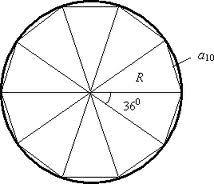 Похожие вопросы:
|