Докажите, что медианы, проведённые к боковым сторонам равнобедренного треугольника равны.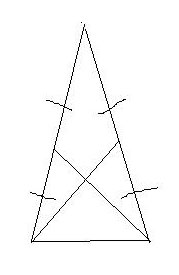

Решение:
Пусть ABC - равноб. тр-к, AC - основание, AM - медиана, опущенная на сторону BC, CN - медиана, опущенная на сторону AB. AN = NB, BM = MC. Т.к. AB = BC, то AN = NB = BM = MC. Рассмотрим треугольники ANC и AMC. Сторона AC - общая, AN = MC, угол NAC = углу MCA, т.к. ABC - равнобедренный. Значит, треугольники ANC и AMC равны по двум сторонам и углу между ними. Следовательно, AM = CN.