| Главная Научный калькулятор | |
|
|
На каждой стороне правильного треугольника, периметр которого равен 18 см, лежат две точки, делящие стороны на три равные части. Вычислите длину меньшей диагонали выпуклого шестиугольника, вершинами которого являются отмеченные точкиРешение: Шестиугольник получается правильный, все его стороны равны 18/3=6 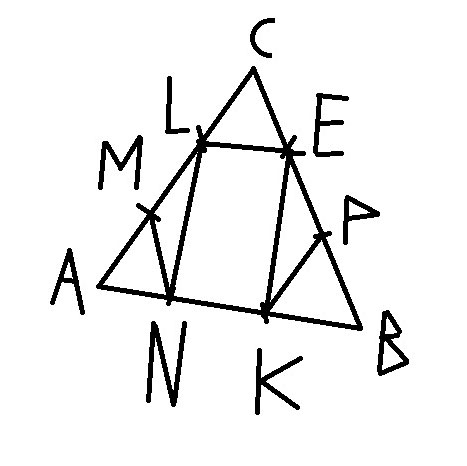 Похожие вопросы:
|