Дано: четырех угольник ABCD;
угол 1 - внешний угол.
Найти: Чему равна сумма внешних углов n-угольника? И от чего она зависит?

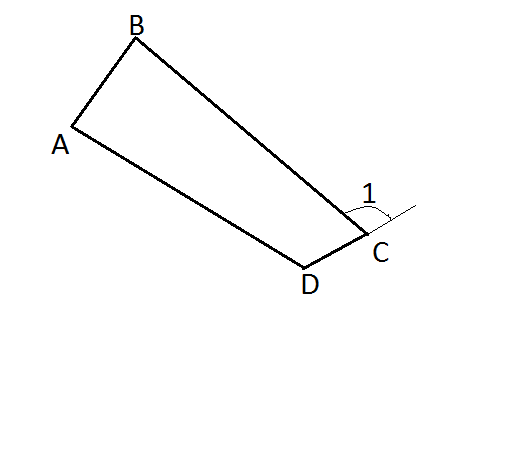Решение:
Сумма внутренних углов выпуклого n - угольника равна 180*(n-2).(это известная теорема геометрии, примем без доказательства). Тогда сумма всех внешних углов выпуклого n - угольника: 180*n - 180*(n-2) = 360 гр.  (так как сумма 2-х смежных углов равна 180 гр) Как видим, сумма внешних углов любого выпуклого n - угольника всегда равна 360 град. И не зависит от n! Для нарисованного 4-ника - также.