|
|
|
Главная
Научный калькулятор
|
|
|
1На координатной плоскости заданы точки : А(-4;1) В(3;3) С(2;0). Найдите координаты точки D если четырёхугольник ABCD является параллелограммом. В ответе укажите наибольшую из координат точки D.
2Известны длины диагоналей ромба АВСД : АС=18, ВД=80. Найдите длину вектора АС+ВД.
Решение: 1. Можно так. Диагонали параллелограмма пересекаются в точке, которая делит их пополам. Найдем середину диагонали АС.
\( x= \frac{-4+2}{2}=-1;y= \frac{1+0}{2}=0,5 \)
Найдем координаты точки D.
\( -1= \frac{3+x_D}{2};x_D=-2-3=-5; 0,5= \frac{3+y_D}{2};y_D=1-3=-2;D(-5;-2). \)
2. \( AC+BD=AC+CK=AK=2AD \)
\( AD= \sqrt{9^{2} +40^{2} }= \sqrt{1681}=41; \)
\( AC+BD=41*2=82 \). 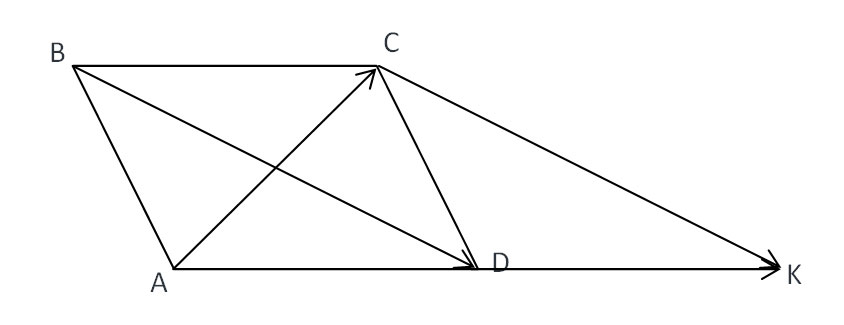 Похожие вопросы:
|