| Главная Научный калькулятор | |
|
|
Квадрат Abcp со стороной 10 см согнули на 90° по диогонали AC.Найдите расстояние между точками B и PРешение: Длина диагоналей AC и BD (NB! диагонали прямоугольника равны) по т.Пифагора равна $$ \\\sqrt{10^2+10^2}=\sqrt{100+100}=\sqrt{2\cdot100}=10\sqrt2 $$ см. Когда квадрат согнули, половинки диагонали BD стали катетами прямоугольного треугольника BOD с катетами BO и OD, равными половине длины BD (NB! диагонали прямоугольника точкой пересечения делятся пополам), т.е. $$ 5\sqrt2 $$ см (см.рис.). Из ΔBOD по т.Пифагора $$ \\BD=\sqrt{BO^2+OD^2}=\sqrt{(5\sqrt2)^2+(5\sqrt2)^2}=\\=\sqrt{25\cdot2+25\cdot2}=\sqrt{50+50}=\sqrt{100}=10 $$ 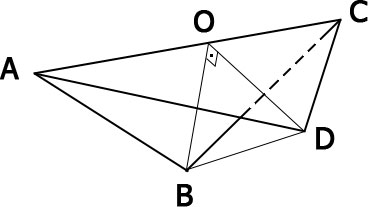 Похожие вопросы:
|