| Главная Научный калькулятор | |
|
|
B треугольнике ABC, известно что AC=BC,AB=15,sinA=4/5 Найдите ACРешение: Пусть СК - медиана (бисектриса, высота) равнобедренного треугольника АВС (АС=ВС) АК=АВ:2 АК=15:2=7.5 так как угол при основании треугольника острый А - острый за основным тригонометрчиеским тождеством cos A=корень(1-sin^2 A) cos A=корень(1-(4/5)^2)=3/5=0.6 по определению косинуса острого угла прямоугольного треугольника (треугольник АСК - прямоугольный, СК -высота треугольника АВС) cos A=AK/AC AC=AK/cos A; AC=7.5/3 * 5=12.5 Вариант 2: sinA=4/5, значит sinA=CK/AC(CK перпенд.AB), тогда пусть CK=4x,AC=5x. По т.ПИфагора AK=3x, 3x=7,5(медиана, высота),x=2,5, тогда AC=12,5 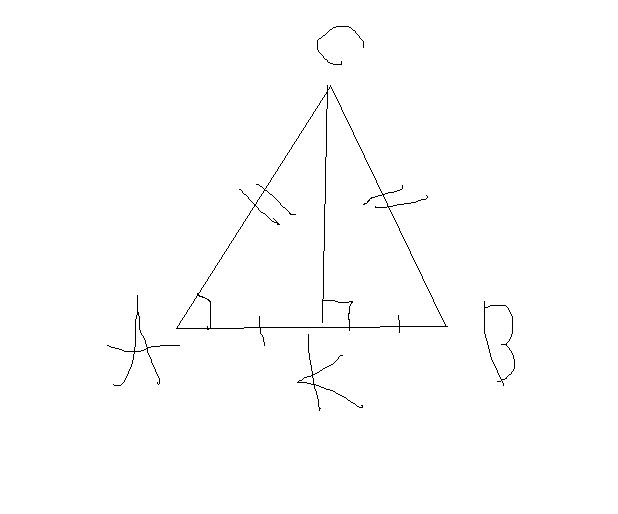 Похожие вопросы:
|