| Главная Научный калькулятор | |
|
|
Средняя линия равнобедренного треугольника, параллельная основанию, равна 16 см, а биссектриса, проведенная к основанию, -30 см. Найдите среднюю линию, параллельную боковой стороне треугольника.Решение: Δ АВС - равнобедренный ВК = 30 см - биссектриса к основанию АС, она же и медиана Δ АВС ⇒ АК=КС NM = 16 см - средняя линия II АС ⇒AN=NB NK = ? - средняя линия II ВС NM x ВК в т.О и деляться ей пополам, т.к. Δ NMB подобен Δ АВС по 3-м углам, ⇒ Δ NMB равнобедренный и ВО его высота, биссектриса и медиана. ВО=ВК т.к. NM средняя линия Δ АВС Получаем NO=1/2NM= 16/2=8 OK=1/2ВК= 30/2=15 Δ NOK прямоугольный, т.к. уже доказано, что BO высота Δ NMB ⇒ BON = 90°; NOK - смежный и =180° - BON = 90° По теореме Пифагора находим NK - гипотенузу Δ NOK NK=√(NO²+OK²) = √(8²+15²)=√(64+225)=√289=17 см 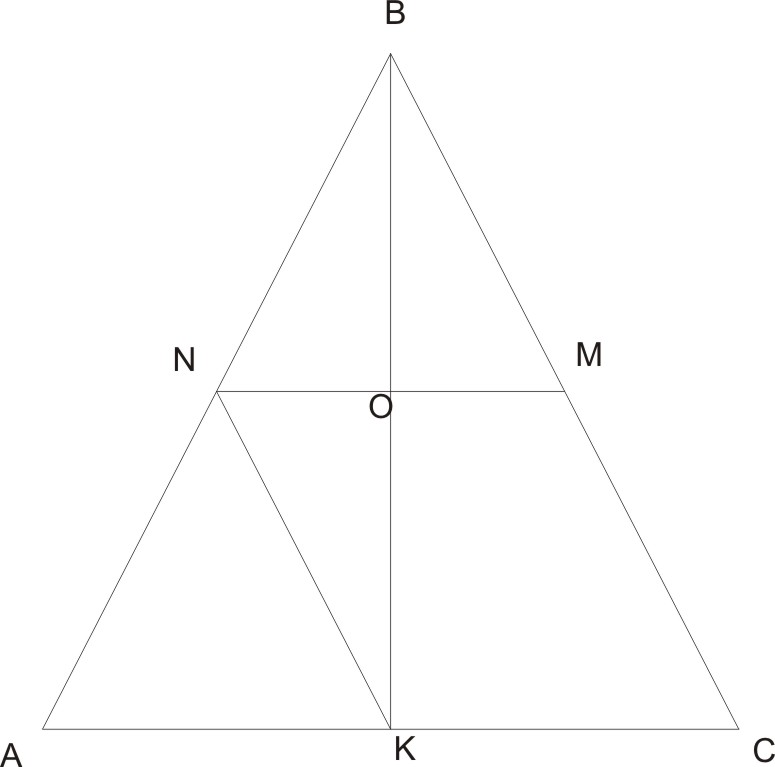 Похожие вопросы:
|