Продолжения боковых сторон трапеции ABCD (рис. 148) пересекаются в точке О. Найдите ВО и отношение площадей треугольников ВОС и AOD, если AD = 5см, ВС = 2см, АО = 25см.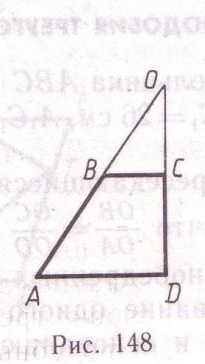

Решение:
треугольники AOD и BOC подобны по трем углам:
уг.AOD-общий
уг.OCB=уг.ODA (они прямые)
уг.OBC=уг.OAD (вытекает из предыдущих равенств)

Т.к. эти треугольники подобны, отношения соответсвующих сторон равны, т.е.
BC/AD=BO/AO
подставляем числа и находим BO:
2/5=BO/25
5*BO=2*25
5*BO=50
BO=10

Теперь находим отношение площадей:
S(BOC)/S(AOD)=(1/2*OC*BC)/(1/2*OD*AD)=OC*BC/OD*AD=OC/OD*BC/AD
BC/AD=2/5
так как отношение соответсвующих сторон равны OC/OD=BC/AD=2/5
S(BOC)/S(AOD)=2/5*2/5=4/25=0,16

Ответ: BO=10, отношение площадей = 0,16.