| Главная Научный калькулятор | |
|
|
Из середины каждой стороны остроугольного треугольника площади S проведены перпендикуляры к двум другим сторонам. Найдите площадь шестиугольника, ограниченного этими перпендикулярами.Решение: Пусть A1, B1 и C1 – середины сторон ВС, АС и АВ соответственно в треугольнике АВС, а H1, H2 и H3 – точки попарного пересечения перпендикуляров, указанных в условии. Так как треугольник АВС – остроугольный, то эти точки лежат внутри треугольника (см. Рис. 4). Средние линии A1B1, B1C1 и C1A1 разбивают исходный треугольник на четыре равных треугольника. Следовательно, площадь треугольника A1B1C1 равна 1\4S 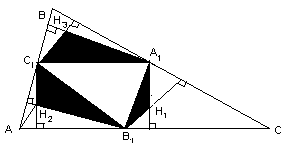 Похожие вопросы:
|