| Главная Научный калькулятор | |
|
|
Найти площадь прямоугольника, если его диагональ, равная 16м, образует со стороной угол в 60 градусовРешение: Диагональ делит прямоугольник на 2 прямоугольных треугольника с гипотенузой, равной длине диагонали - 16м. Треуг. ACD: (см. рисунок) sinA = CD/AC, CD= sinA*AC CD = sin60°*16 = $$ 8\sqrt{3} $$. Тогда AD найдем по теореме Пифагора: AD = $$ \sqrt{16^2-(8\sqrt{3})^2} = \sqrt{256-64*3} = \sqrt{64} = 8 $$ S = AD*CD = $$ 8*8\sqrt{3} = 64\sqrt{3} $$. Ответ: $$ 64\sqrt{3} $$ 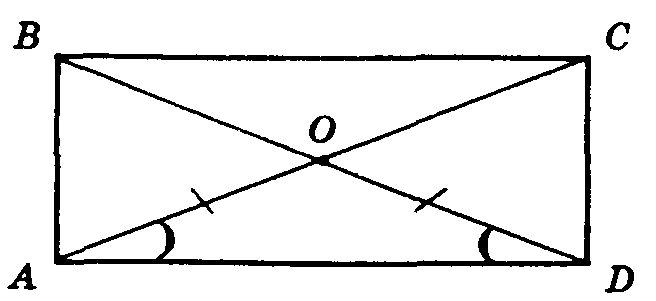 Похожие вопросы:
|