| Главная Научный калькулятор | |
|
|
Хорда длиной 6 корней из 3 см делит дугу окружности в отношении 1:2. Найдите длину большей из двух образовавшихся дугРешение: Центральный угол, который опирается на хорду из условия: a = 360/3 = 120 град. Если на концы хорды провести радиусы, то из получившегося равнобедренного тр-ка - очевидно: 6кор3 = 2Rsina/2 = 2Rsin60 = Rкор3 R = 6 Тогда длина всей окружности: С = 2ПR = 12П. Тогда большая дуга по длине равна (2/3)*С = 8П Ответ: 8П a=6√3 см x+2x=2πr 3x=2πr r=3x/2π x=αr x=α(3x/2π) α=x/(3x/2π) α=x*2π/3x α=2π/3 радусов=2π/3*180/π=120 градусов sin½α=½a/r sin½*120=½*6√3/r sin60=3√3/r √3/2=3√3/r 6√3=r√3 r=6 см 6=3x/2π 3x=12π x=4π 2x=8π 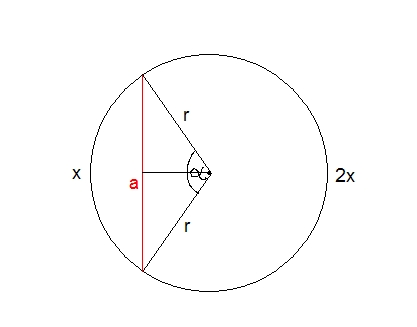 Похожие вопросы:
|